import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import statsmodels.api as sm
loans = pd.read_csv('data/loans_full_schema.csv')AE 11: Modelling loan interest rates
In this application exercise we will be studying loan interest rates. The dataset is one you’ve come across before in your reading – the dataset about loans from the peer-to-peer lender, Lending Club, from the openintro R package. We will use pandas and scikit-learn for data exploration and modeling, respectively.
Before we use the dataset, we’ll make a few transformations to it.
- Your turn: Review the code below and write a summary of the data transformation pipeline.
Add response here.
loans['credit_util'] = loans['total_credit_utilized'] / loans['total_credit_limit']
loans['bankruptcy'] = loans['public_record_bankrupt'].apply(lambda x: 0 if x == 0 else 1).astype('category')
loans['verified_income'] = loans['verified_income'].astype('category')
loans['homeownership'] = loans['homeownership'].str.title().astype('category')
loans['homeownership'] = pd.Categorical(loans['homeownership'], categories=["Rent", "Mortgage", "Own"], ordered=True)
loans = loans.rename(columns={'inquiries_last_12m': 'credit_checks'})
loans = loans[['interest_rate', 'loan_amount', 'verified_income', 'debt_to_income', 'credit_util', 'bankruptcy', 'term', 'credit_checks', 'issue_month', 'homeownership']]Here is a glimpse at the data:
print(loans.info())
print(loans.describe())<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10000 entries, 0 to 9999
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 interest_rate 10000 non-null float64
1 loan_amount 10000 non-null int64
2 verified_income 10000 non-null category
3 debt_to_income 9976 non-null float64
4 credit_util 9998 non-null float64
5 bankruptcy 10000 non-null category
6 term 10000 non-null int64
7 credit_checks 10000 non-null int64
8 issue_month 10000 non-null object
9 homeownership 10000 non-null category
dtypes: category(3), float64(3), int64(3), object(1)
memory usage: 576.7+ KB
None
interest_rate loan_amount debt_to_income credit_util term \
count 10000.000000 10000.000000 9976.000000 9998.000000 10000.000000
mean 12.427524 16361.922500 19.308192 0.403158 43.272000
std 5.001105 10301.956759 15.004851 0.269313 11.029877
min 5.310000 1000.000000 0.000000 0.000000 36.000000
25% 9.430000 8000.000000 11.057500 0.169029 36.000000
50% 11.980000 14500.000000 17.570000 0.360192 36.000000
75% 15.050000 24000.000000 25.002500 0.607317 60.000000
max 30.940000 40000.000000 469.090000 1.835280 60.000000
credit_checks
count 10000.00000
mean 1.95820
std 2.38013
min 0.00000
25% 0.00000
50% 1.00000
75% 3.00000
max 29.00000 Get to know the data
- Your turn: What is a typical interest rate in this dataset? What are some attributes of a typical loan and a typical borrower. Give yourself no more than 5 minutes for this exploration and share 1-2 findings.
# add code to explore loans here# add code to explore borrowers hereInterest rate vs. credit utilization ratio
Python does not encode categories or handle missing values for you. Linear regression models are incapable of handling either, so we will need to use one-hot encoding to encode categories and drop missing values.
Hint: Python also does not convert the one-hot encoded values to numerics… so we must do this as well.
X = loans[['credit_util', 'homeownership']]
X = pd.get_dummies(X, drop_first=True)
X = X.dropna()
X = X.replace([np.inf, -np.inf], np.nan).dropna()
X = X.astype(float)
y = loans.loc[X.index, 'interest_rate']
y = y.dropna()The regression model for interest rate vs. credit utilization is as follows.
X = sm.add_constant(X)
model = sm.OLS(y, X).fit()
print(model.summary2()) Results: Ordinary least squares
=====================================================================
Model: OLS Adj. R-squared: 0.068
Dependent Variable: interest_rate AIC: 59859.3779
Date: 2025-05-05 17:48 BIC: 59888.2185
No. Observations: 9998 Log-Likelihood: -29926.
Df Model: 3 F-statistic: 243.7
Df Residuals: 9994 Prob (F-statistic): 1.25e-152
R-squared: 0.068 Scale: 23.309
---------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
---------------------------------------------------------------------
const 9.9250 0.1401 70.8498 0.0000 9.6504 10.1996
credit_util 5.3356 0.2074 25.7266 0.0000 4.9291 5.7421
homeownership_Mortgage 0.6956 0.1208 5.7590 0.0000 0.4588 0.9323
homeownership_Own 0.1283 0.1552 0.8266 0.4085 -0.1760 0.4326
---------------------------------------------------------------------
Omnibus: 1150.070 Durbin-Watson: 1.981
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1616.376
Skew: 0.900 Prob(JB): 0.000
Kurtosis: 3.800 Condition No.: 6
=====================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors
is correctly specified.And here is the model visualized:
sns.scatterplot(x='credit_util', y='interest_rate', data=loans, alpha=0.5)
sns.lineplot(x=loans['credit_util'], y=model.predict(X), color='red')
plt.xlabel('Credit Utilization')
plt.ylabel('Interest Rate')
plt.title('Interest Rate vs. Credit Utilization')
plt.show()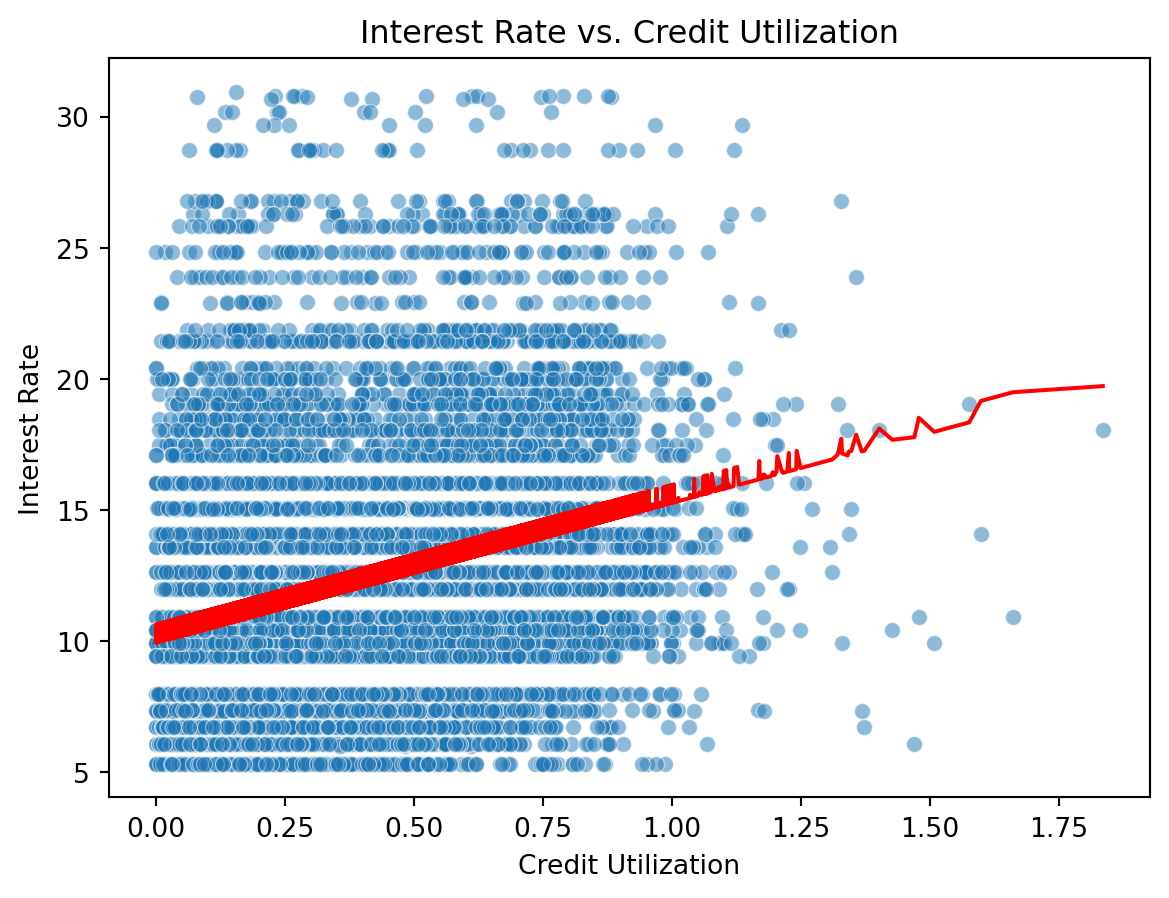
- Your turn: Interpret the intercept and the slope.
Add response here.
Interest rate vs. homeownership
Next we predict interest rates from homeownership, which is a categorical predictor with three levels:
homeownership_levels = loans['homeownership'].cat.categories
print(homeownership_levels)Index(['Rent', 'Mortgage', 'Own'], dtype='object')- Fit the linear regression model to predict interest rate from homeownership and display a summary of the model. Write the estimated model output below.
# add code here- Your turn: Interpret each coefficient in context of the problem.
Add response here.
Interest rate vs. credit utilization and homeownership
Main effects model
- Fit a model to predict interest rate from credit utilization and homeownership, without an interaction effect between the two predictors. Display the summary output and write out the estimated regression equation.
# add code hereAdd response here.
- Write the estimated regression equation for loan applications from each of the homeownership groups separately.
- Rent: Add response here.
- Mortgage: Add response here.
- Own: Add response here.
- Question: How does the model predict the interest rate to vary as credit utilization varies for loan applicants with different homeownership status. Are the rates the same or different?
Add response here.
Interaction effects model
- Fit a model to predict interest rate from credit utilization and homeownership, with an interaction effect between the two predictors. Display the summary output and write out the estimated regression equation.
# add code hereAdd response here.
- Write the estimated regression equation for loan applications from each of the homeownership groups separately.
- Rent: Add response here.
- Mortgage: Add response here.
- Own: Add response here.
- Question: How does the model predict the interest rate to vary as credit utilization varies for loan applicants with different homeownership status. Are the rates the same or different?
Add response here.
Choosing a model
Rule of thumb: Occam’s Razor - Don’t overcomplicate the situation! We prefer the simplest best model.
# add code here- Review: What is R-squared? What is adjusted R-squared?
Add response here.
- Question: Based on the adjusted
Add response here.
Another model to consider
- Your turn: Let’s add one more model to the variable – issue month. Should we add this variable to the interaction effects model from earlier?
# add code hereAdd response here.
