AE 04: NYC flights + data preprocessing

Suggested answers

Application exercise
Answers
Important

These are suggested answers. This document should be used as reference only, it’s not designed to be an exhaustive key.

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, MaxAbsScaler, MinMaxScaler
import numpy as np
from nycflights13 import flights

Exercise 1 - Load data

Fill in the blanks:

# Load the flights data
df = flights
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 336776 entries, 0 to 336775
Data columns (total 19 columns):
 #   Column          Non-Null Count   Dtype  
---  ------          --------------   -----  
 0   year            336776 non-null  int64  
 1   month           336776 non-null  int64  
 2   day             336776 non-null  int64  
 3   dep_time        328521 non-null  float64
 4   sched_dep_time  336776 non-null  int64  
 5   dep_delay       328521 non-null  float64
 6   arr_time        328063 non-null  float64
 7   sched_arr_time  336776 non-null  int64  
 8   arr_delay       327346 non-null  float64
 9   carrier         336776 non-null  object 
 10  flight          336776 non-null  int64  
 11  tailnum         334264 non-null  object 
 12  origin          336776 non-null  object 
 13  dest            336776 non-null  object 
 14  air_time        327346 non-null  float64
 15  distance        336776 non-null  int64  
 16  hour            336776 non-null  int64  
 17  minute          336776 non-null  int64  
 18  time_hour       336776 non-null  object 
dtypes: float64(5), int64(9), object(5)
memory usage: 48.8+ MB

The flights data frame has 336776 rows. Each row represents a observation.

Exercise 2 - Data cleaning

Remove rows with missing values in the arr_delay and distance columns.

What are the names of the variables in flights.

df_clean = df.dropna(subset=['arr_delay', 'distance'])

Exercise 3 - Original Data Distribution

  • Plot the original distributions of arr_delay and distance.
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
sns.histplot(df_clean['arr_delay'], bins=30, kde=True, ax=axes[0]).set(title='Original Arrival Delay')
sns.histplot(df_clean['distance'], bins=30, kde=True, ax=axes[1]).set(title='Original Distance')
plt.tight_layout()
plt.show()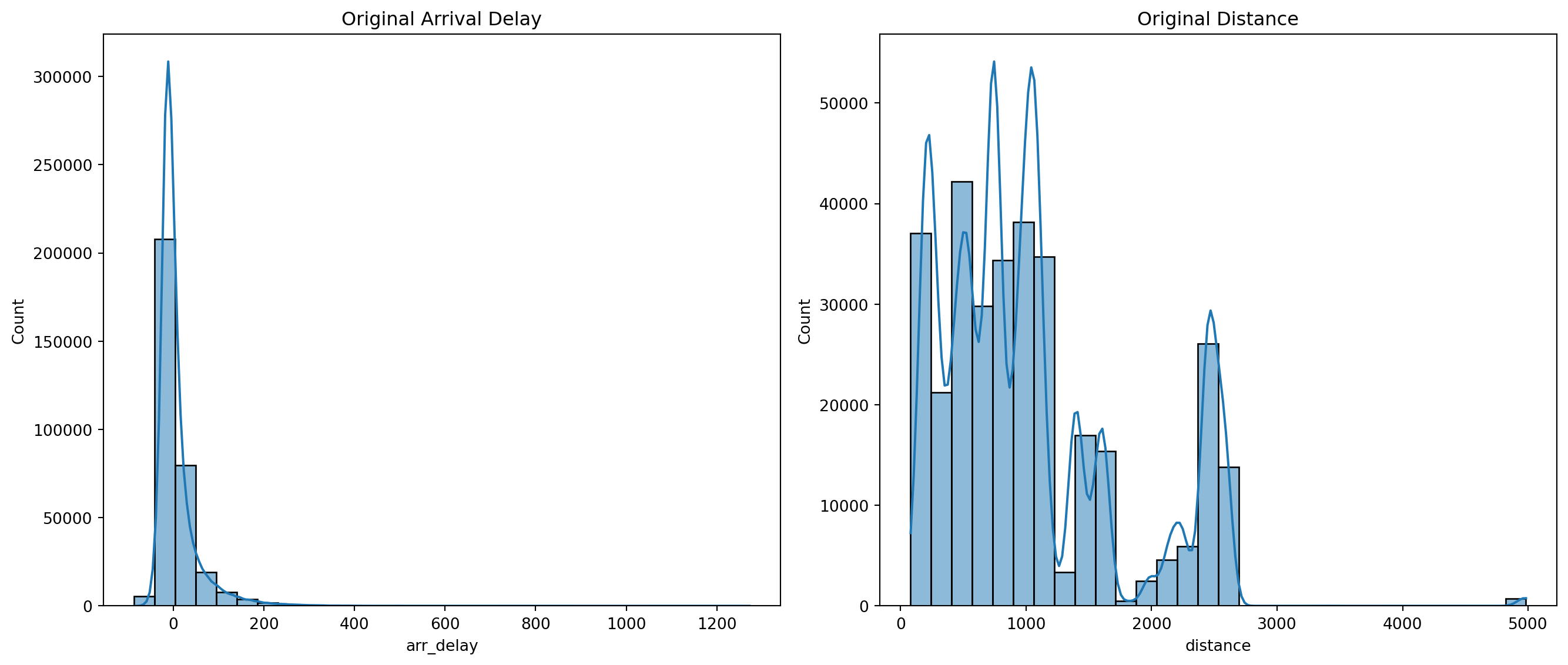

Exercise 4 - Check for Skewness

  • Calculate and print the skewness of arr_delay and distance.
skew_arr_delay = df_clean['arr_delay'].skew()
skew_distance = df_clean['distance'].skew()
print(f"Skewness of Arrival Delay: {skew_arr_delay}")
print(f"Skewness of Distance: {skew_distance}")
Skewness of Arrival Delay: 3.716817480457187
Skewness of Distance: 1.1133926208294944

Exercise 5 - Scaling

  • Check the summary statistics of arr_delay and distance to see if scaling is necessary.
df_clean['arr_delay'].describe()
count    327346.000000
mean          6.895377
std          44.633292
min         -86.000000
25%         -17.000000
50%          -5.000000
75%          14.000000
max        1272.000000
Name: arr_delay, dtype: float64
df_clean['distance'].describe()
count    327346.000000
mean       1048.371314
std         735.908523
min          80.000000
25%         509.000000
50%         888.000000
75%        1389.000000
max        4983.000000
Name: distance, dtype: float64
  • Question: Do arr_delay and distance need to be scaled?

Yes, the units are completely different.

  • Apply standard scaling, maximum absolute scaling, and Min-Max Scaling to the transformed arr_delay and distance.
# Standard Scaling
scaler = StandardScaler()
df_clean.loc[:, ['arr_delay_standard', 'distance_standard']] = scaler.fit_transform(df_clean[['arr_delay', 'distance']])

# Maximum Absolute Scaling
max_abs_scaler = MaxAbsScaler()
df_clean.loc[:, ['arr_delay_maxabs', 'distance_maxabs']] = max_abs_scaler.fit_transform(df_clean[['arr_delay', 'distance']])

# Min-Max Scaling
min_max_scaler = MinMaxScaler()
df_clean.loc[:, ['arr_delay_minmax', 'distance_minmax']] = min_max_scaler.fit_transform(df_clean[['arr_delay', 'distance']])
  • Question: What are the two pros and two cons of standardizing data?

Pros

  1. Improved Model Performance:

    • Consistency: Ensures that features contribute equally to the model, enhancing performance for algorithms like linear regression and neural networks.

    • Speed: Helps optimization algorithms, like gradient descent, converge faster.

  2. Enhanced Interpretability:

    • Standardization: Makes model coefficients easier to understand, especially in linear models.

    • Comparison: Simplifies comparison between features during data analysis.

Cons

  1. Potential Loss of Interpretability:

    • Raw Values: Scaled values might lose their original meaning and units.

  2. Assumption of Distribution:

    • Normality: Some methods assume data is normally distributed, which may not always be true.

    • Sensitive to Outliers: Outliers can distort scaled values in methods like standard scaling.

Exercise 6 - Transformation

  • Check the summary statistics again with your min-max standardized columns.
df_clean['arr_delay_minmax'].describe()
count    327346.000000
mean          0.068406
std           0.032867
min           0.000000
25%           0.050810
50%           0.059647
75%           0.073638
max           1.000000
Name: arr_delay_minmax, dtype: float64
df_clean['distance_minmax'].describe()
count    327346.000000
mean          0.197506
std           0.150094
min           0.000000
25%           0.087497
50%           0.164797
75%           0.266979
max           1.000000
Name: distance_minmax, dtype: float64
  • Question: Why should you use the min-max scaled data instead of a different scaling for the transformations (hint: especially log transformation)

The other transformations had with negative values for arr_delay.

  • Apply a log transformation to arr_delay if it is positively skewed and apply a square root transformation to distance if it is negatively skewed (use if else statements).

  • Hint: Logical operators in Python:

    operator definition
    < is less than?
    <= is less than or equal to?
    > is greater than?
    >= is greater than or equal to?
    == is exactly equal to?
    != is not equal to?
    x and y is x AND y?
    x or y is x OR y?
    pd.isna(x) is x NA?
    ~pd.isna(x) is x not NA?
    x in y is x in y?
    x not in y is x not in y?
    not x is not x? (only makes sense if x is True or False) 
if skew_arr_delay > 0:
    df_clean.loc[:, 'arr_delay_transformed'] = np.log1p(df_clean['arr_delay_minmax'])
else:
    df_clean.loc[:, 'arr_delay_transformed'] = df_clean['arr_delay_minmax']

if skew_distance > 0:
    df_clean.loc[:, 'distance_transformed'] = np.sqrt(df_clean['distance_minmax'])
else:
    df_clean.loc[:, 'distance_transformed'] = df_clean['distance_minmax']
  • Question: Why do we have to add a constant when we perform a log or square-root transformation (i.e., np.log1p(df['column' + 1]))?

The logarithmic and square-root functions do not contain negative numbers or 0.