Linear algebra I

Lecture 22

Dr. Greg Chism

University of Arizona
INFO 511 - Fall 2024

Linear algebra

Linear algebra

  • Linear algebra is the study of vectors, vector spaces, and linear transformations.

  • Fundamental to many fields including data science, machine learning, and statistics.

Vectors

Vectors

Definition:

  • Vectors are objects that can be added together and multiplied by scalars to form new vectors. In a data science context, vectors are often used to represent numeric data.

Examples:

  • Three-dimensional vector: [height, weight, age] = [70, 170, 40]

  • Four-dimensional vector: [exam1, exam2, exam3, exam4] = [95, 80, 75, 62]

Vectors in Python

import numpy as np
v = np.array([3, 2])
print(v)
[3 2]
Code 
import matplotlib.pyplot as plt
import numpy as np

v = np.array([3, 2])
origin = np.array([0, 0])

plt.quiver(*origin, *v, scale=1, scale_units='xy', angles='xy')
plt.xlim(0, 4)
plt.ylim(0, 3)
plt.grid()
plt.show()

Vector addition

  • Vectors of the same length can be added or subtracted componentwise.

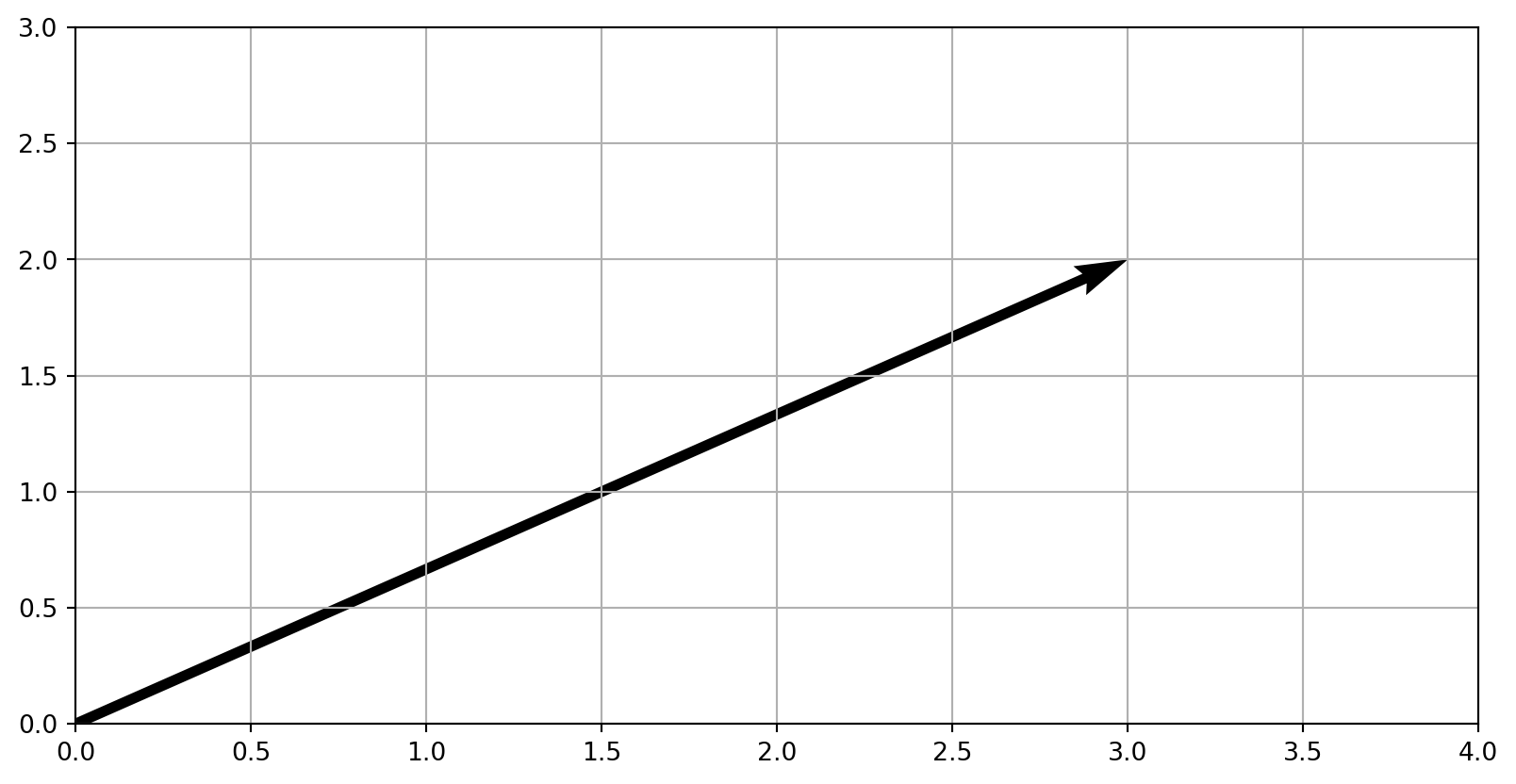
  • Example: \(\mathbf{v} = [3,2]\) and \(\mathbf{w}=[2,-1]\)

  • Result: \(\mathbf{v}+\mathbf{w}=[5,1]\)

v = np.array([3, 2])
w = np.array([2, -1])
v_plus_w = v + w
print(v_plus_w) 
[5 1]
Code 
v = np.array([3, 2])
w = np.array([2, -1])
v_plus_w = v + w

plt.quiver(*origin, *v, color='r', scale=1, scale_units='xy', angles='xy')
plt.quiver(*origin, *w, color='b', scale=1, scale_units='xy', angles='xy')
plt.quiver(*origin, *v_plus_w, color='g', scale=1, scale_units='xy', angles='xy')
plt.xlim(0, 6)
plt.ylim(-2, 3)
plt.grid()
plt.show()

Vector subtraction

  • Vectors of the same length can be added or subtracted componentwise.

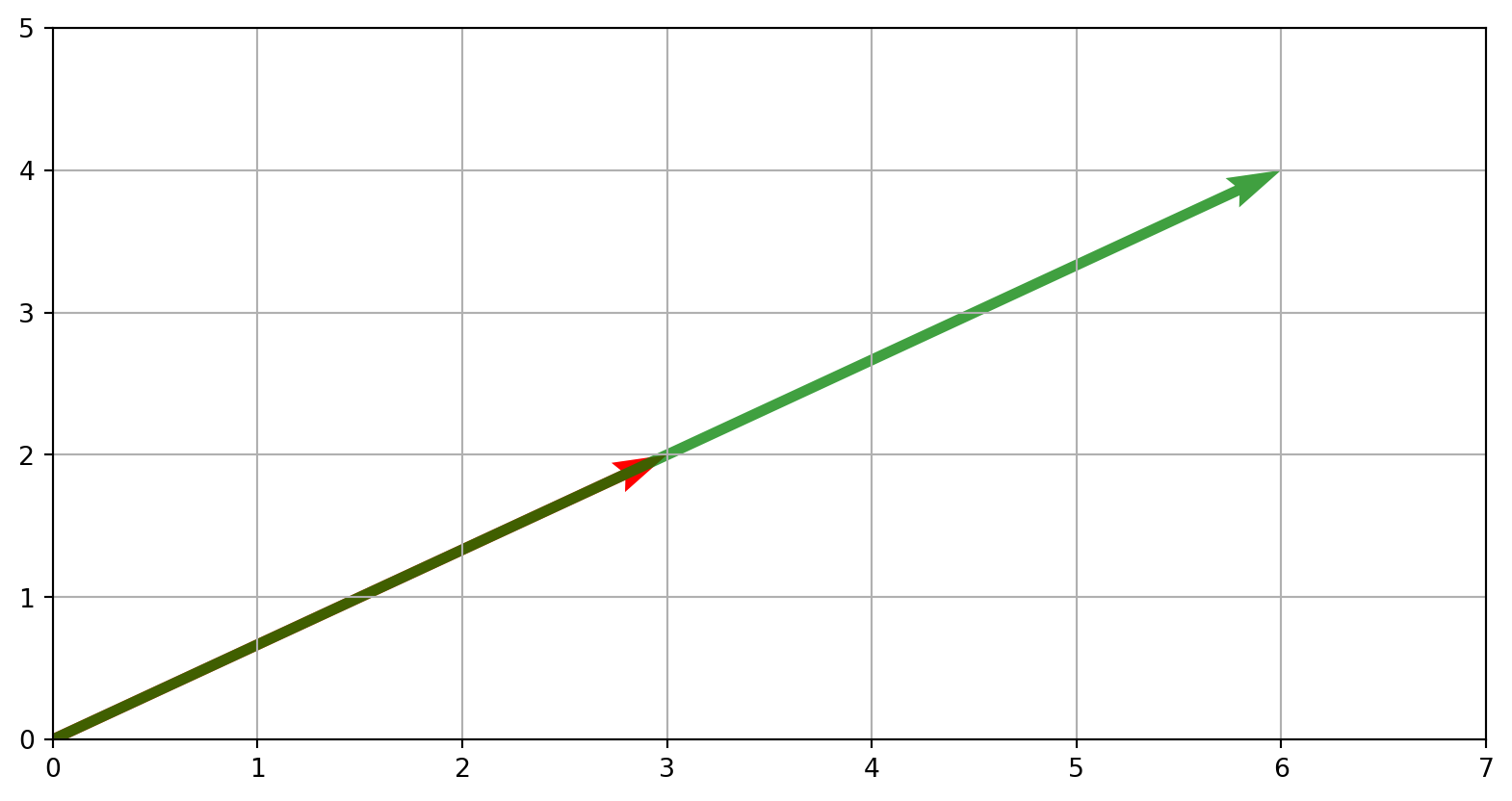
  • Example: \(\mathbf{v} = [3,2]\) and \(\mathbf{w}=[2,-1]\)

  • Result: \(\mathbf{v}-\mathbf{w}=[1,3]\)

v = np.array([3, 2])
w = np.array([2, -1])
v_plus_w = v - w
print(v_plus_w) 
[1 3]
Code 
v = np.array([3, 2])
w = np.array([2, -1])
v_plus_w = v - w

plt.quiver(*origin, *v, color='r', scale=1, scale_units='xy', angles='xy')
plt.quiver(*origin, *w, color='b', scale=1, scale_units='xy', angles='xy')
plt.quiver(*origin, *v_plus_w, color='g', scale=1, scale_units='xy', angles='xy')
plt.xlim(0, 6)
plt.ylim(-2, 3)
plt.grid()
plt.show()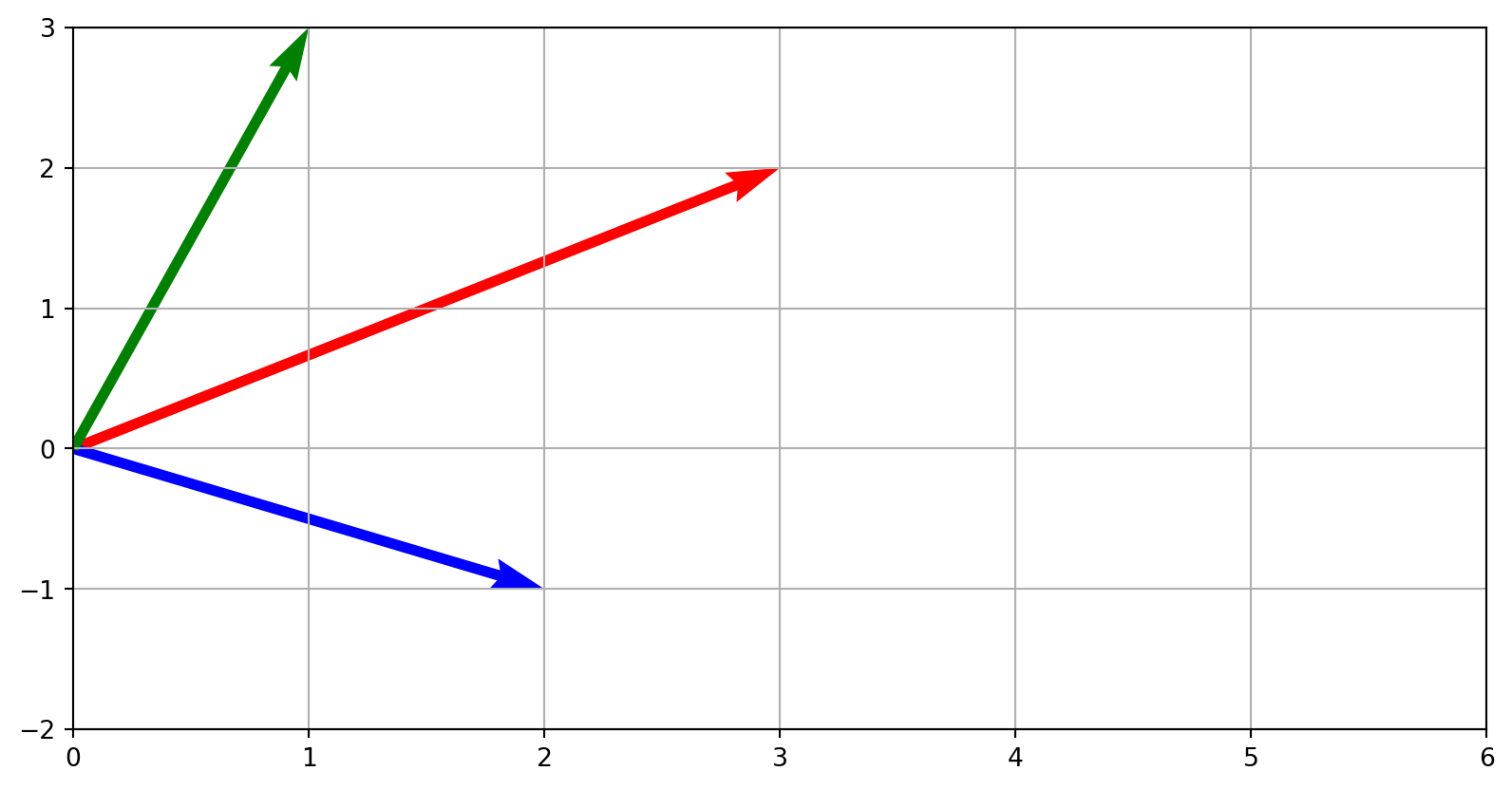

Vector scaling

  • Scaling vector \(\mathbf{v}=[3,2]\) by \(2\)

  • Result: \([6,4]\)

v = np.array([3, 2])
scaled_v = 2.0 * v
print(scaled_v)
[6. 4.]
Code 
scaled_v = 2 * v

plt.quiver(*origin, *v, color='r', scale=1, scale_units='xy', angles='xy')
plt.quiver(*origin, *scaled_v, color='g', scale=1, scale_units='xy', angles='xy', alpha=0.75)
plt.xlim(0, 7)
plt.ylim(0, 5)
plt.grid()
plt.show()

Linearly independent and span

Span

The span of a set of vectors \(\mathbf{v1},\mathbf{v2},...,\mathbf{vn}\) is the set of all linear combinations of the vectors.

i.e., all the vectors \(\mathbf{b}\) for which the equation \([\mathbf{v1} \space \mathbf{v2} \space... \space\mathbf{vn}]\mathbf{x=b}\)

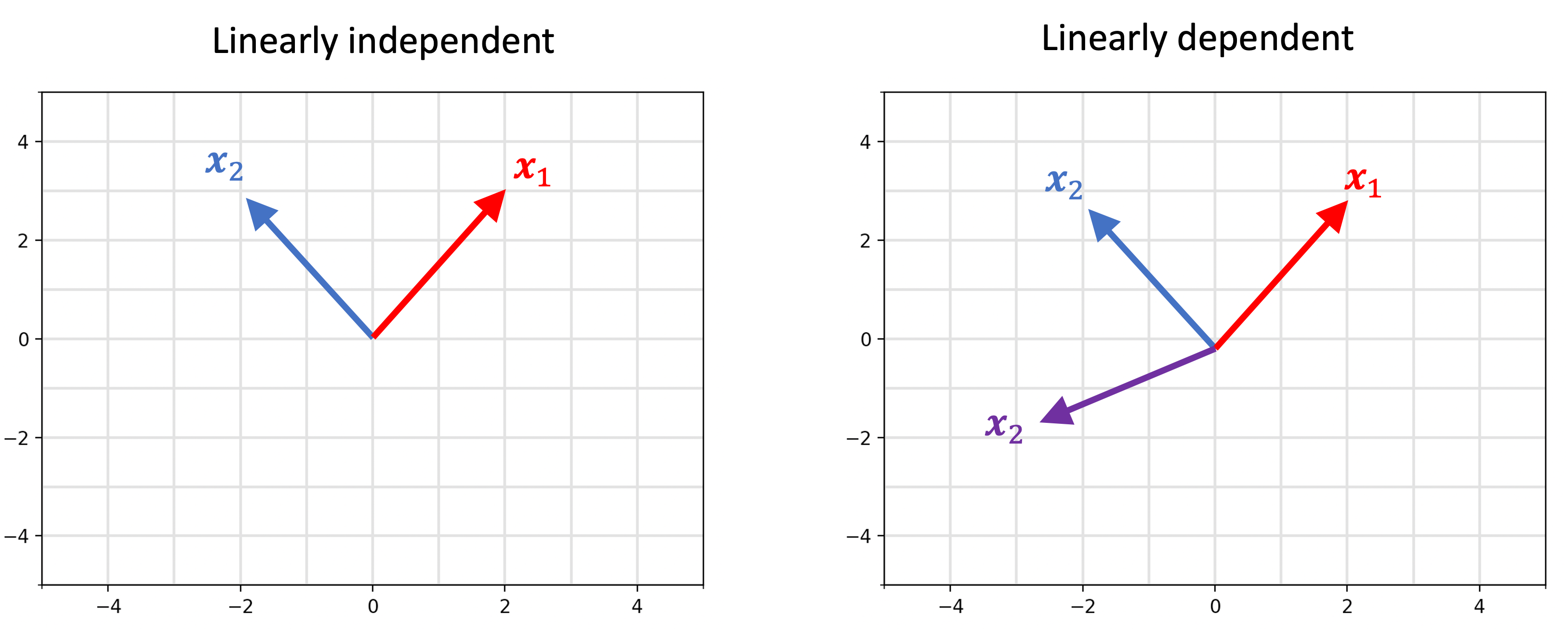
Linear independent vs. dependent

Vectors are linearly independent if each vector lies outside the span of the remaining vectors. Otherwise, the vectors are said to be linearly dependent1.

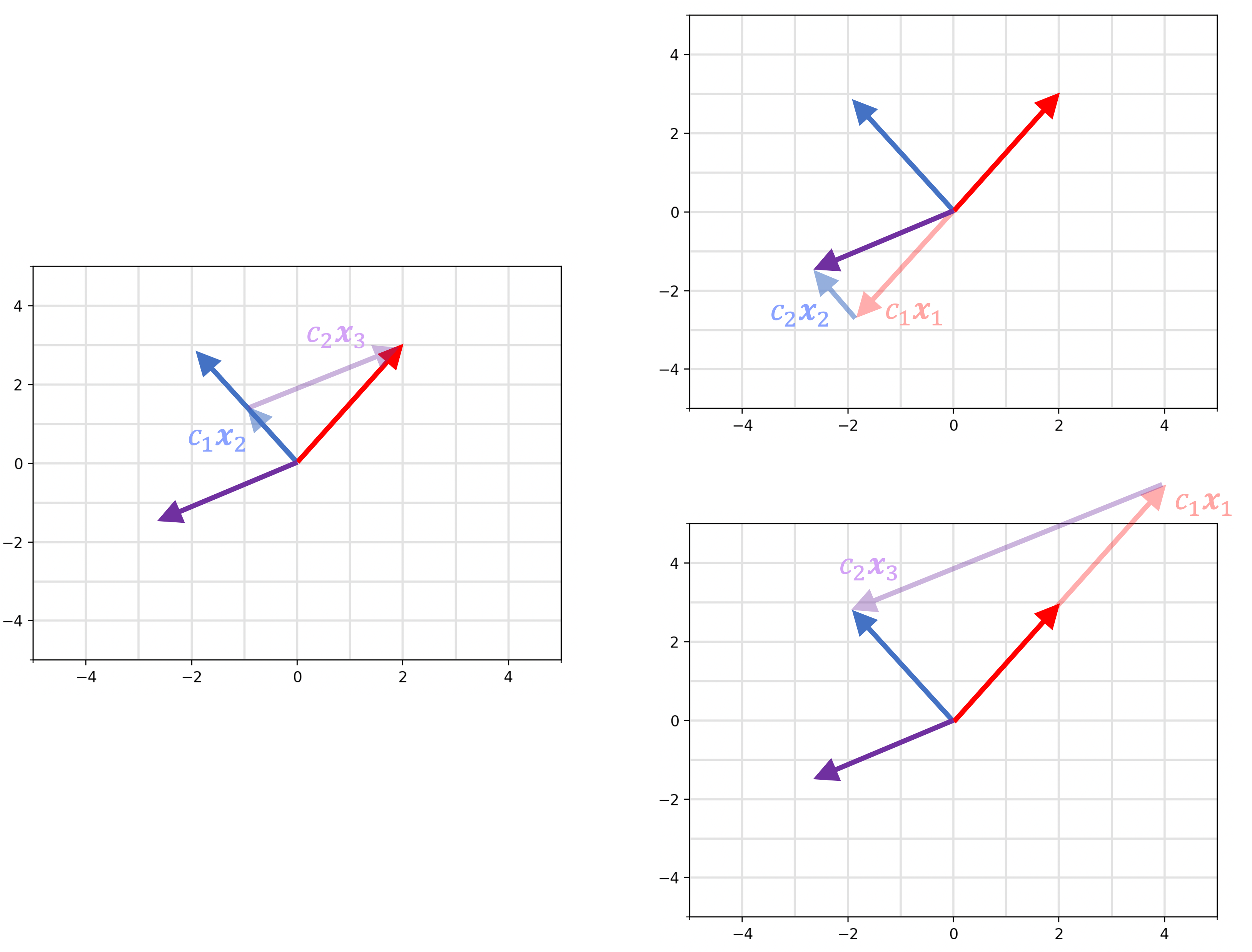
Linear independent vs. dependent

The vector on th right can be constructed by any two combination of the other vectors.

Matrices

Matrices

  • Matrices are collections of vectors arranged in rows and columns.

  • Represent linear transformations.

  • Example Matrix:

\[ \mathbf{A} = \begin{bmatrix}3 & 0 \\0 & 2 \end{bmatrix} \]

A = np.array([[3,0],[0,2]])
print(A)
[[3 0]
 [0 2]]

Matrix transposition

  • Matrix transposition involves swapping the rows and columns.

  • Notation: If \(\mathbf{A}\) is a matrix, then its transpose is denoted as \(\mathbf{A}^T\).

  • Given the matrix \(\mathbf{A}\):

\[ \mathbf{A}= \begin{bmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\a_{31} & a_{32} & a_{33}\end{bmatrix} \]

  • The matrix \(\mathbf{A}^T\) is:

\[ \mathbf{A}^T=\begin{bmatrix}a_{11} & a_{21} & a_{31}\\a_{12} & a_{22} & a_{32}\\a_{13} & a_{23} & a_{33}\end{bmatrix} \]

Matrix transposition: Python

Code 
import numpy as np

# Original matrix
A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

# Transpose of the matrix
A_T = A.T

print("Original Matrix:")
print(A)
print("\nTransposed Matrix:")
print(A_T)
Original Matrix:
[[1 2 3]
 [4 5 6]
 [7 8 9]]

Transposed Matrix:
[[1 4 7]
 [2 5 8]
 [3 6 9]]

Matrix-vector multiplication

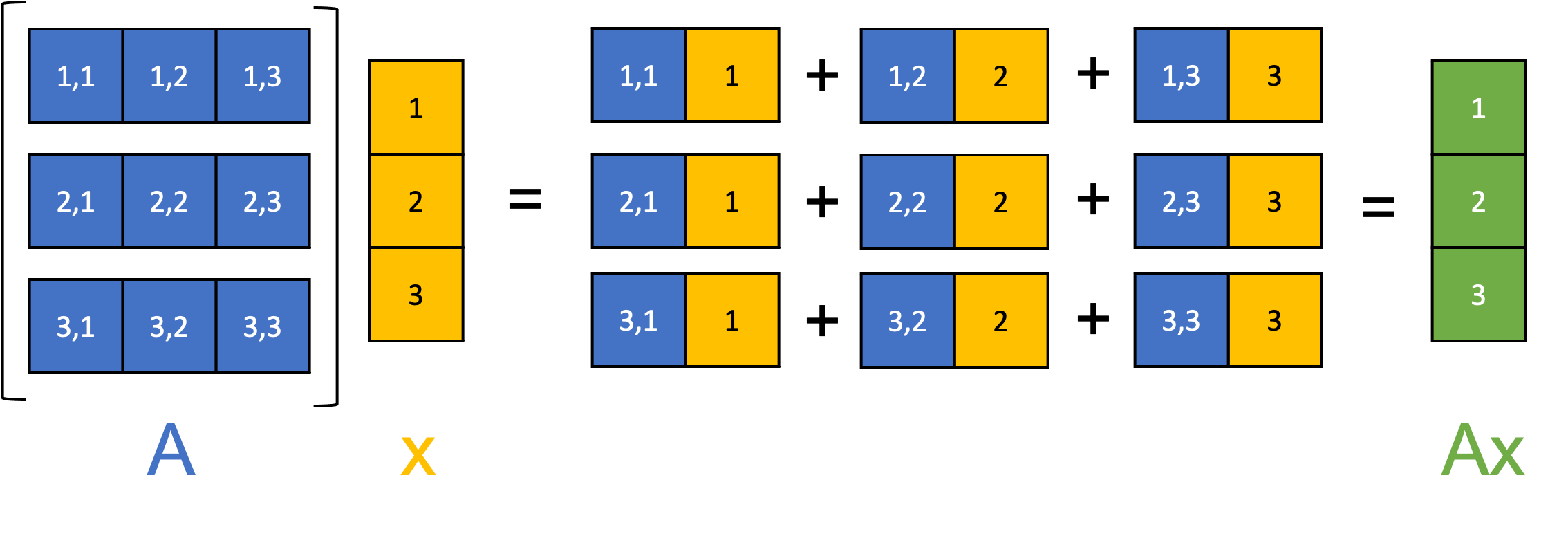
Matrix-vector multiplication

Geometrically

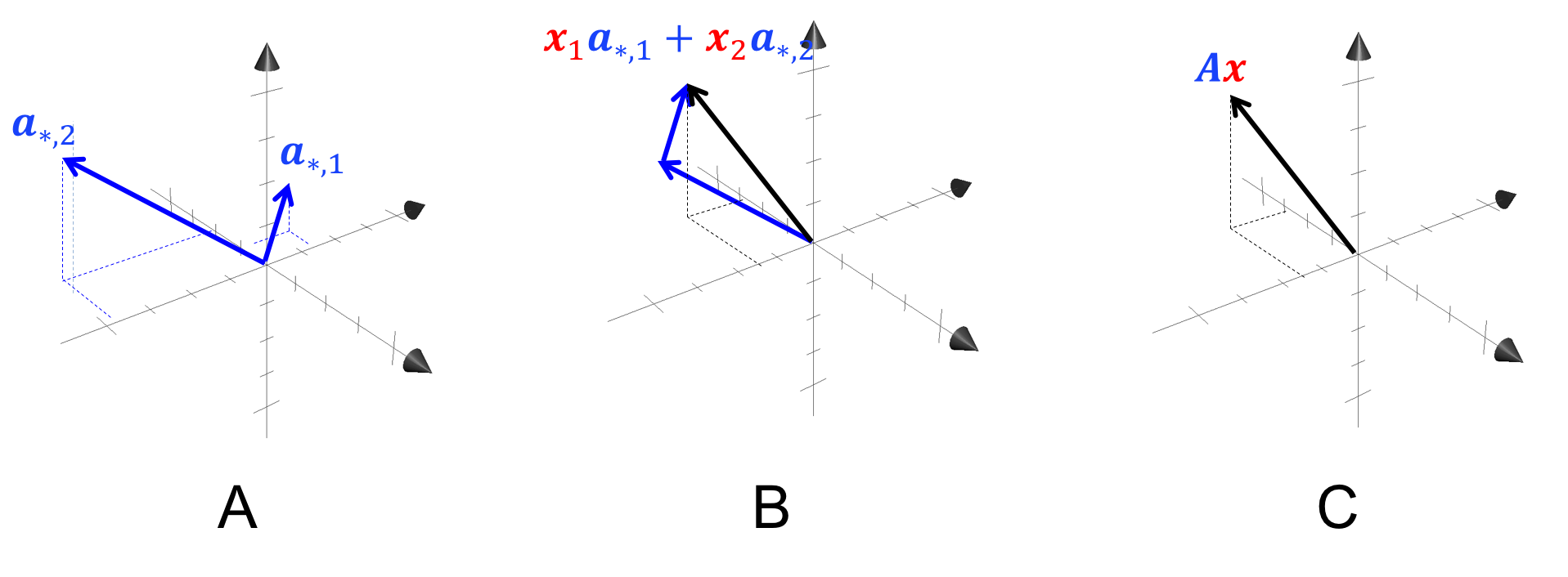
Matrix-vector multiplication

  • Matrix-vector multiplication transforms the vector according to the basis vectors of the matrix.

  • Formula: \(\mathbf{A} \cdot \mathbf{v}\)

\[ \mathbf{A} \cdot \mathbf{v} = \begin{bmatrix}3 & 0 \\0 & 2 \end{bmatrix} \cdot [3, 2] \]

A = np.array([[3,0],[0,2]])
v = np.array([3, 2])
new_v = A.dot(v)
print(new_v) 
[9 4]
Code 
A = np.array([[3, 0], [0, 2]])
v = np.array([3, 2])
new_v = A.dot(v)

plt.quiver(*origin, *v, color='r', scale=1, scale_units='xy', angles='xy')
plt.quiver(*origin, *new_v, color='g', scale=1, scale_units='xy', angles='xy')
plt.xlim(0, 10)
plt.ylim(0, 5)
plt.grid()
plt.show()

Determinants

The determinant is a function that maps square matrices to real numbers: \(\text{Det}:ℝ^{m×m}→ℝ\)

where the absolute value of the determinant describes the volume of the parallelepided formed by the matrix’s columns.

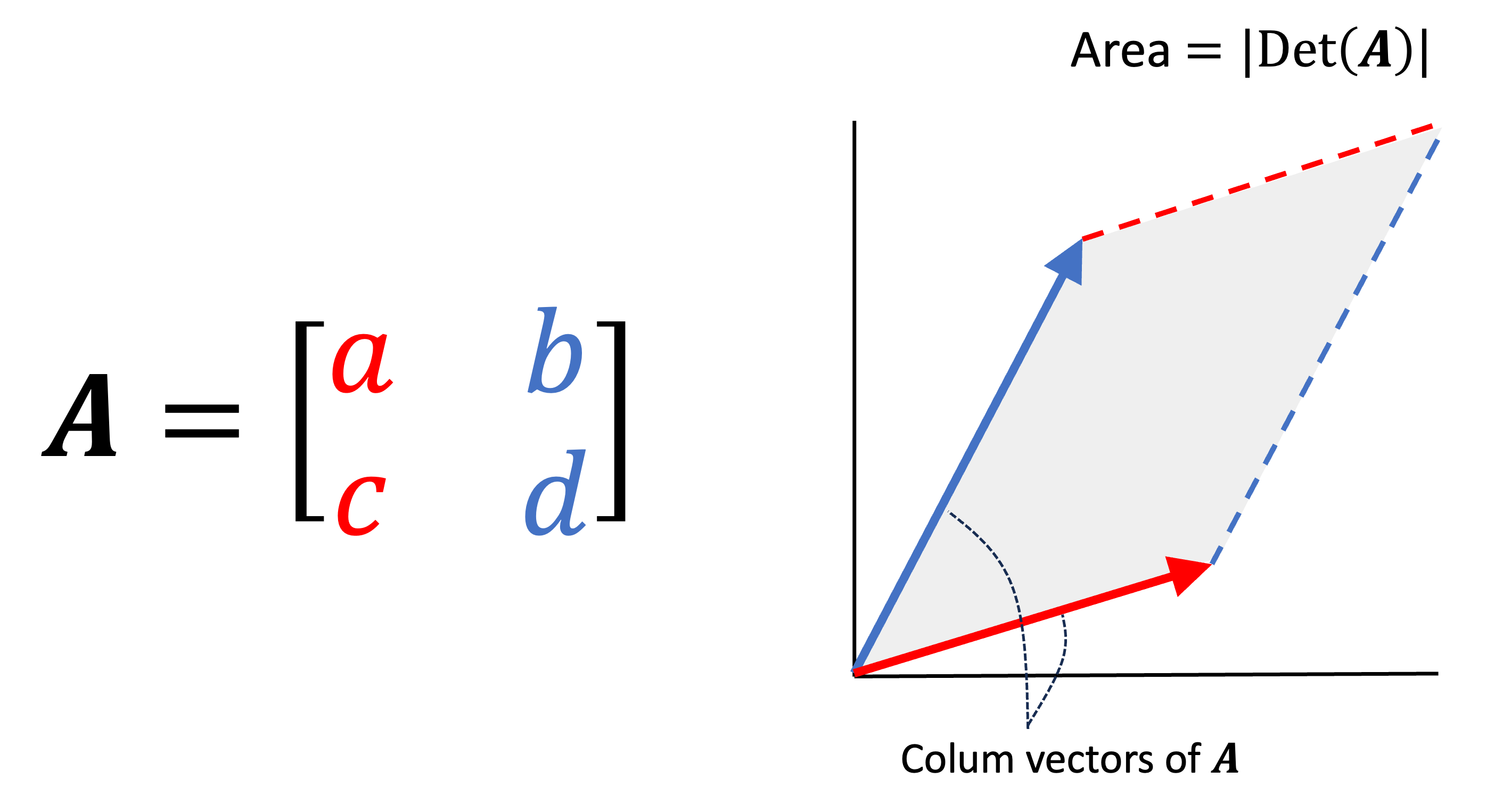
Determinants: Python

  • Determinants measure the scale factor of a transformation.

  • Determinant of 0 indicates linear dependence.

from numpy.linalg import det
A = np.array([[3, 0], [0, 2]])
determinant = det(A)
print(determinant)
6.0

ae-15-linear-algebra

Practice matrix operations (you will be tested on this in Exam 2)

🔗 datasciaz.netlify.app