from sympy import symbols, integrate
x = symbols('x')
f = x**2 + 1
area = integrate(f, (x, 0, 1))
print(area) # Output: 4/34/3Calculus II
Lecture 21
Dr. Greg Chism
University of Arizona
INFO 511 - Spring 2025
Summary of Derivative Rules
Differentiation rules
Constant rule: ddx(c)=0
Power rule: ddx(xn)=nxn−1
Constant multiple rule: ddx[c⋅f(x)]=c⋅f′(x)
Sum rule: ddx[f(x)+g(x)]=f′(x)+g′(x)
Difference rule: ddx[f(x)−g(x)]=f′(x)−g′(x)
Integrals
Integration
From last time:
Measures the accumulation of quantities and the area under a curve.
Example: Used to compute the area under probability distribution functions, which is essential in statistics and data analysis.
Symbol: ∫f(x)dx
Practical Application: Calculating Cumulative Distribution Functions (CDFs)
Accumulating quantities
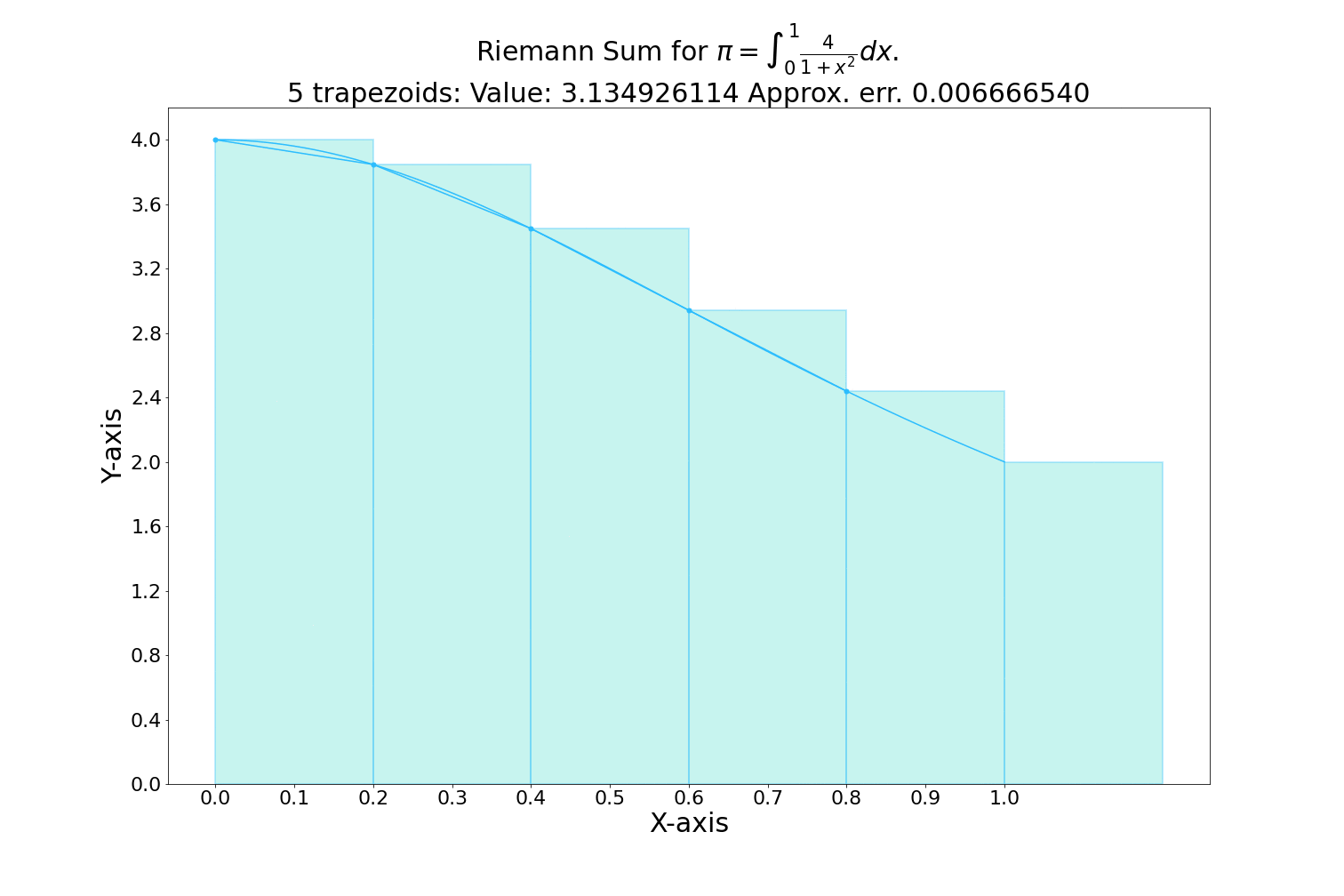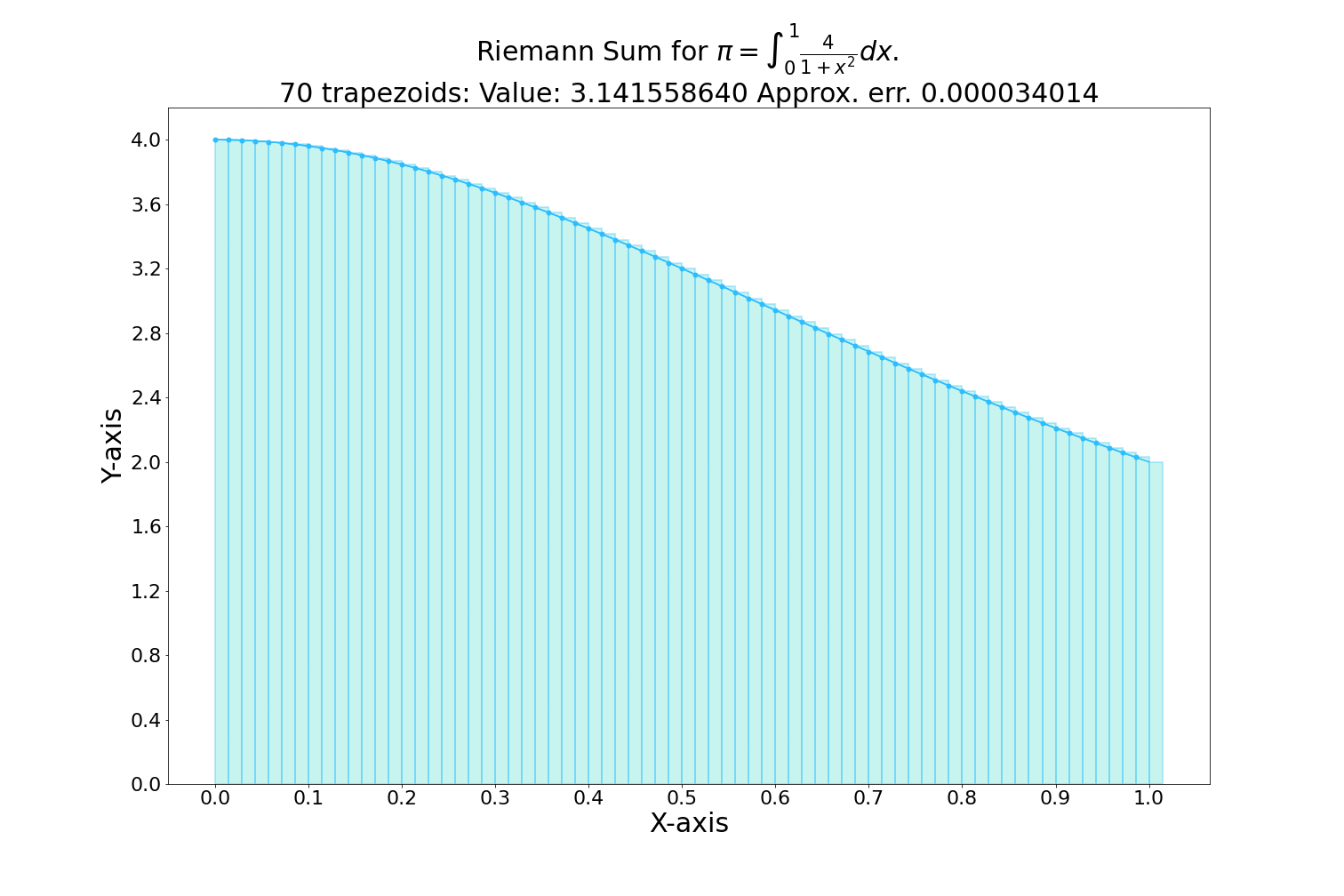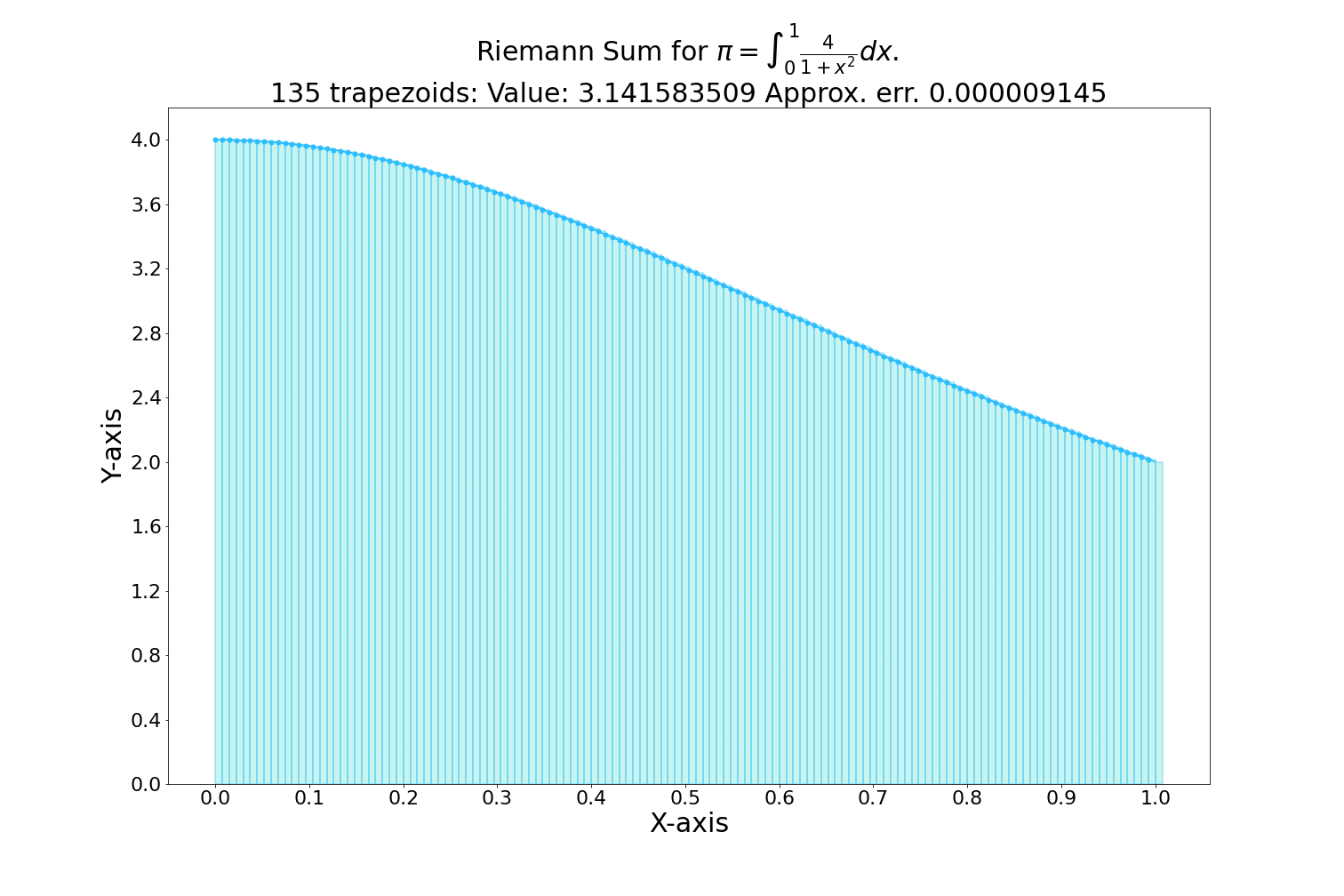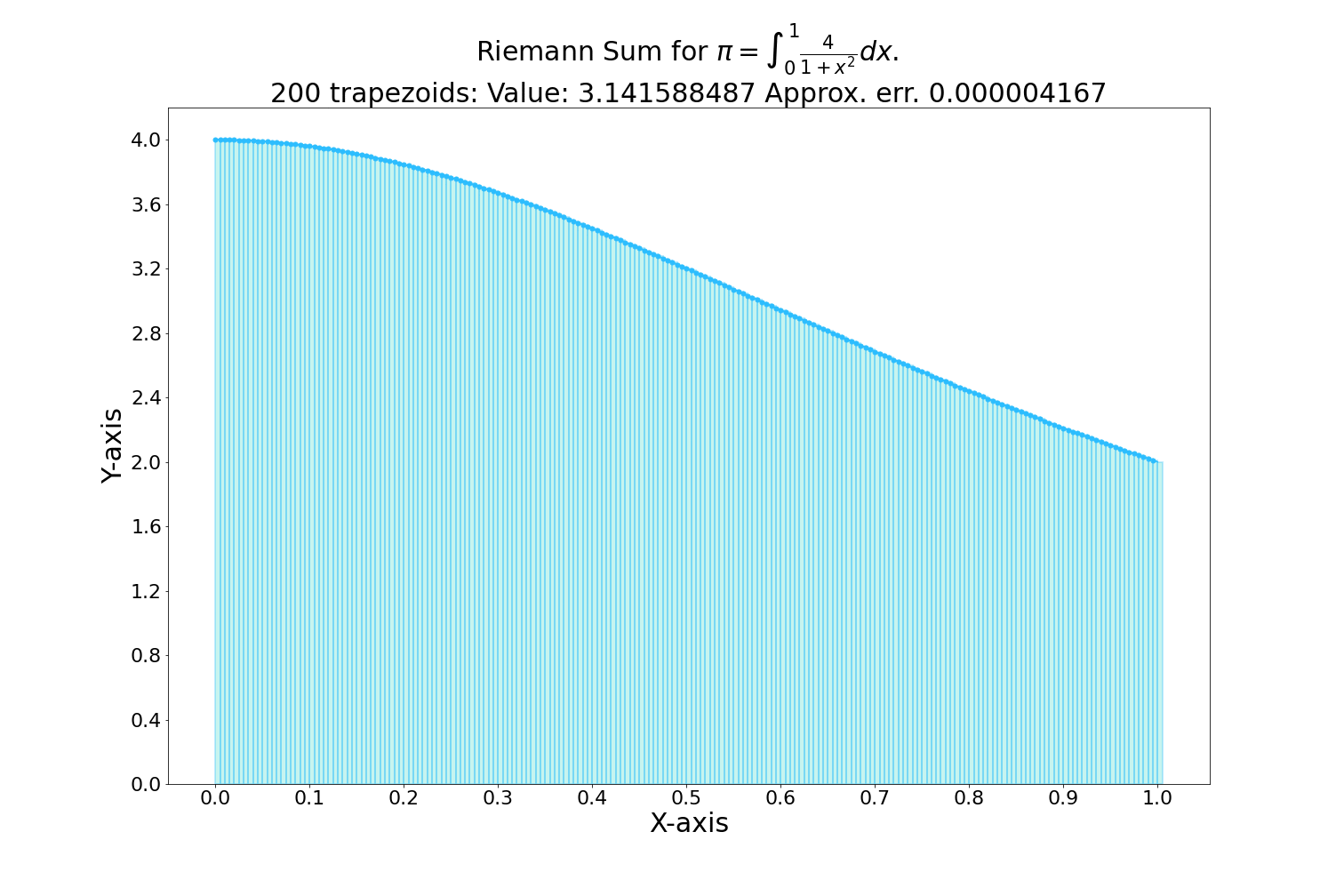
Area under the curve
The integral of a function represents the area under the curve of that function on a graph, between two points.
Example: Finding the total distance traveled given a speed-time graph.
The integral
Integrals in Python
Calculating integrals using SymPy
Solving integrals
Integration rules
Constant rule: ∫c,dx=cx+C
Power rule: ∫xn,dx=xn+1n+1+C
Constant multiple rule: ∫c⋅f(x),dx=c⋅∫f(x),dx
Sum rule: ∫[f(x)+g(x)],dx=∫f(x),dx+∫g(x),dx
Difference rule: ∫[f(x)−g(x)],dx=∫f(x),dx−∫g(x),dx
Example 1: Integrating a Constant
Function: f(x)=7
Integral: ∫7,dx=7x+C
Example 2: Power rule
Function: f(x)=x3
Integral: ∫x3,dx=x44+C
Example 3: Constant multiple rule
Function: f(x)=5x2
Integral: ∫5x2,dx=5⋅x33+C=5x33+C
Example 4: Sum and difference rule
Function: f(x)=x3+4x−5
Integral: ∫(x3+4x−5),dx=x44+2x2−5x+C
Solving complex integrals
Complex Integrals:
Involves functions composed of multiple simpler functions.
Requires application of rules like integration by parts and substitution for integration.
Example Function:
∫ba(ecx+1xn)dx
- Objective: Find the integral
Integration by parts
∫u dv=uv−∫v du
- Used when integrating the product of two functions.
Integration by parts
Function: ∫xex,dx
- Identify the functions
u=x⇒du=dx
dv=ex,dx⇒v=ex
- Apply Integration by Parts
∫xex dx=xex−∫ex dx=xex−ex+C
Integration by parts: Example
Function: ∫xex dx
- Identify the functions
- Let u=x and dv=ex dx
- Differentiate and integrate
Differentiate: u:du=dx
Integrate: dv:v=ex
Integration by parts: Example
Function: ∫xex dx
- Apply the integration by parts formula
∫u dv=uv−∫v du
- Substitute the values
∫xexdx=xex−∫exdx
Integration by parts: Example
Function: ∫xex dx
- Simplify the integral
∫xexdx=xex−ex+C
- Final answer
∫xexdx=ex(x−1)+C
Integration by substitution
Function: ∫f(g(x))g′(x)dx=∫f(u) du
- Used when integrating a composite function.
Integration by substitution: Example 1
Function: ∫2x√x2+1,dx
- Identify the substitution
- Let u=x2+1⇒du=2x,dx
- Apply the substitution
∫2x√x2+1 dx=∫√u du=23(x2+1)3/2+C
Integration by substitution: Example 2
Function: ∫xln(x),dx
- Identify the functions
u=ln(x)⇒du=1x,dx
dv=x,dx⇒v=x22
Integration by substitution: Example 2
Function: ∫xln(x),dx
- Apply integration by parts
∫xln(x),dx=x22ln(x)−∫x22⋅1x dx=x22ln(x)−12∫x dx
=x22ln(x)−x24+C
Regularization
You’ll learn more about this in INFO 521: Introduction to Machine Learning and/or INFO 523: Data Mining and Discovery
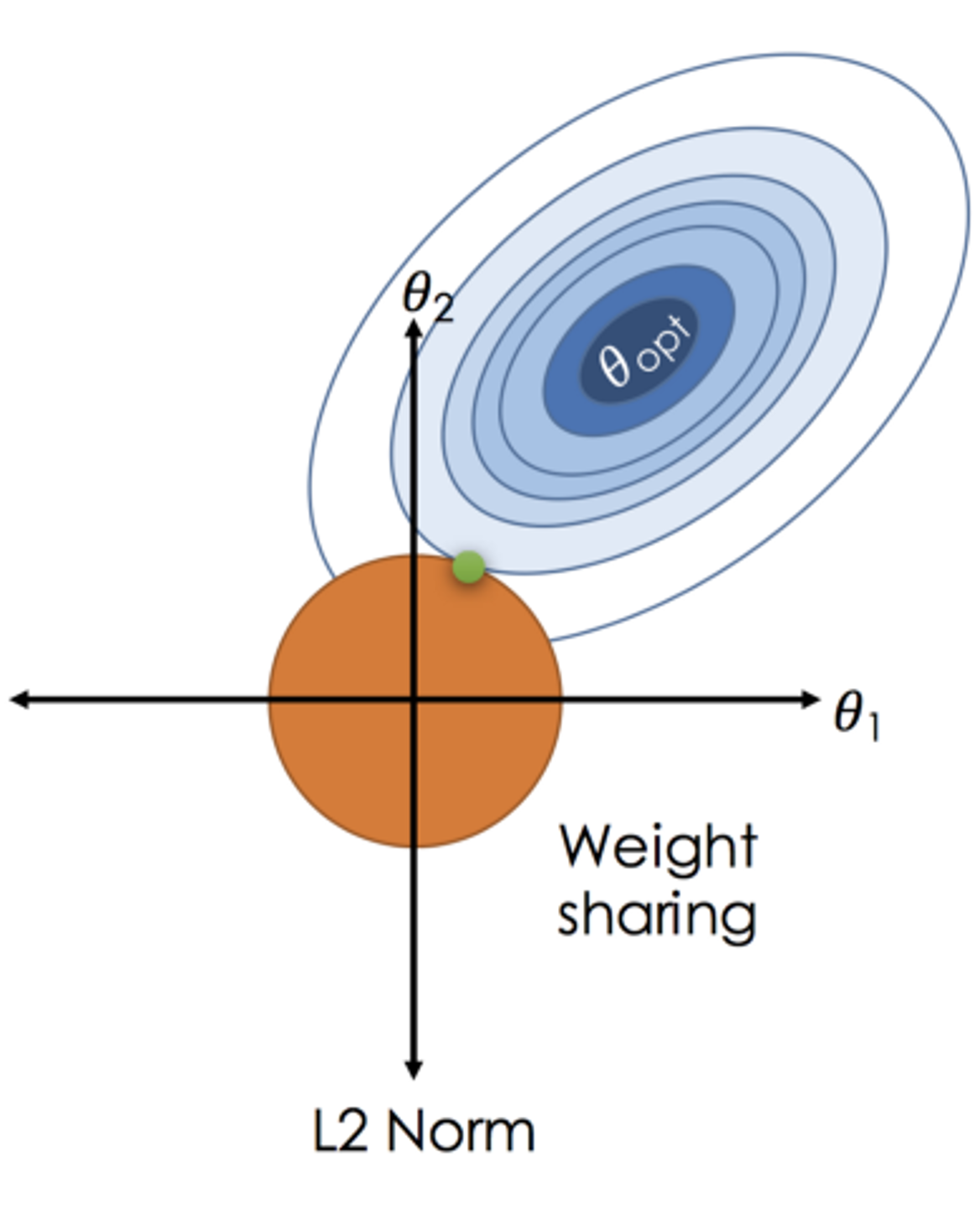
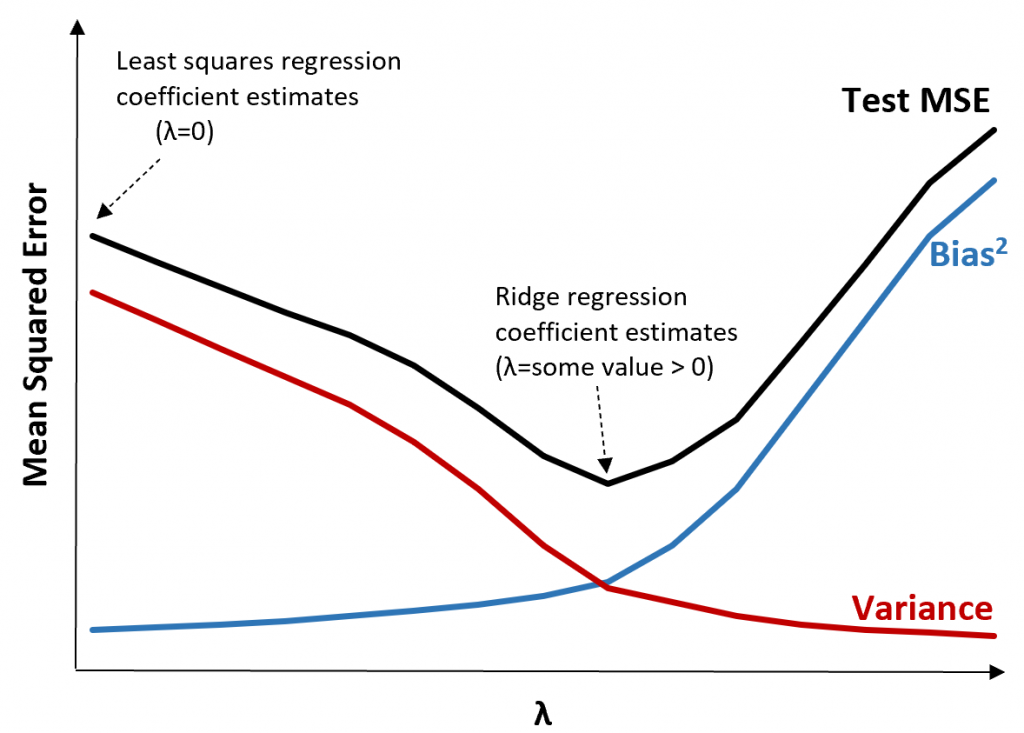
ae-14-integration
Practice integration (you will be tested on this in Exam 2)
Calculus II Lecture 21 Dr. Greg Chism University of Arizona INFO 511 - Spring 2025