Model validation

Lecture 19

Dr. Greg Chism

University of Arizona
INFO 511 - Fall 2024

Setup

import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.model_selection import train_test_split, KFold
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme(style="whitegrid", rc={"figure.figsize": (8, 6), "axes.labelsize": 16, "xtick.labelsize": 14, "ytick.labelsize": 14})

Data: Candy Rankings

candy_rankings = pd.read_csv("data/candy_rankings.csv")

candy_rankings.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 85 entries, 0 to 84
Data columns (total 13 columns):
 #   Column            Non-Null Count  Dtype  
---  ------            --------------  -----  
 0   competitorname    85 non-null     object 
 1   chocolate         85 non-null     bool   
 2   fruity            85 non-null     bool   
 3   caramel           85 non-null     bool   
 4   peanutyalmondy    85 non-null     bool   
 5   nougat            85 non-null     bool   
 6   crispedricewafer  85 non-null     bool   
 7   hard              85 non-null     bool   
 8   bar               85 non-null     bool   
 9   pluribus          85 non-null     bool   
 10  sugarpercent      85 non-null     float64
 11  pricepercent      85 non-null     float64
 12  winpercent        85 non-null     float64
dtypes: bool(9), float64(3), object(1)
memory usage: 3.5+ KB

Model validation

Overfitting

The data we are using to construct our models come from a larger population.
Ultimately we want our model to tell us how the population works, not just the sample we have.
If the model we fit is too tailored to our sample, it might not perform as well with the remaining population. This means the model is “overfitting” our data.
We measure this using model validation techniques.
Note: Overfitting is not a huge concern with linear models with low level interactions, however it can be with more complex and flexible models. The following is just an example of model validation, even though we’re using it in a scenario where the concern for overfitting is not high.

Model validation

One commonly used model validation technique is to partition your data into training and testing set
That is, fit the model on the training data
And test it on the testing data
Evaluate model performance using \(RMSE\), root-mean squared error

\[ RMSE = \sqrt{\frac{\sum_{i = 1}^n (y_i - \hat{y}_i)^2}{n}} \]

Do you think we should prefer low or high RMSE?

Random sampling and reproducibility

Gotta set a seed!

np.random.seed(1234)

Use different seeds from each other
Need inspiration? https://www.random.org/

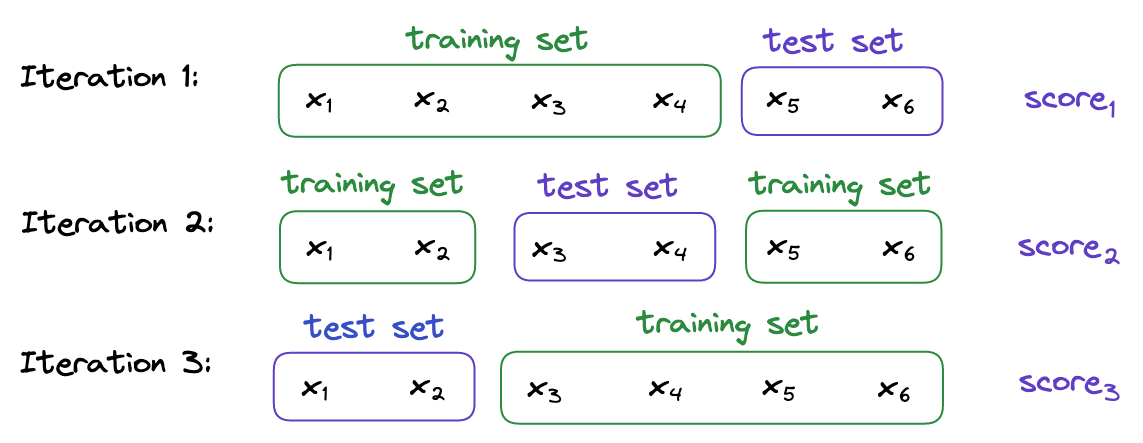
Cross validation

More specifically, k-fold cross validation

Split your data into k folds.
Use 1 fold for testing and the remaining (k - 1) folds for training.
Repeat k times.

Prepping your data for 5-fold CV

candy_rankings['id'] = np.arange(len(candy_rankings))
candy_rankings = candy_rankings.sample(frac=1).reset_index(drop=True)
candy_rankings['fold'] = (np.arange(len(candy_rankings)) % 5) + 1

candy_rankings_cv = candy_rankings.groupby('fold').size().reset_index(name='count')
print(candy_rankings_cv)

   fold  count
0     1     17
1     2     17
2     3     17
3     4     17
4     5     17

CV 1

test_fold = 1
test = candy_rankings[candy_rankings['fold'] == test_fold]
train = candy_rankings[candy_rankings['fold'] != test_fold]

model = smf.ols('winpercent ~ chocolate + fruity + peanutyalmondy + crispedricewafer + hard + sugarpercent', data=train).fit()
rmse_test1 = np.sqrt(mean_squared_error(test['winpercent'], model.predict(test)))
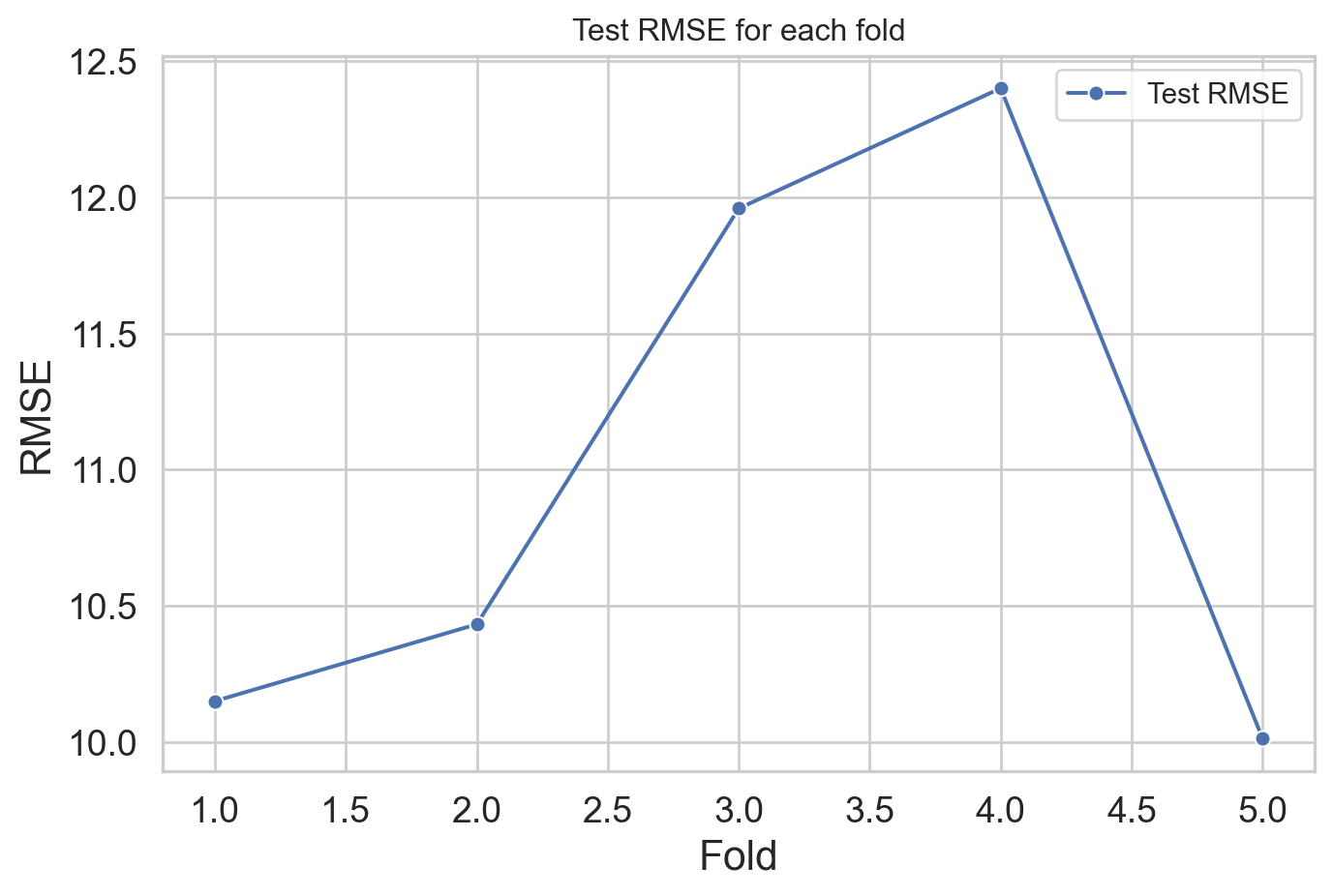
print(f'RMSE Test 1: {rmse_test1}')

RMSE Test 1: 10.15009006066606

RMSE on training vs. testing

Would you expect the RMSE to be higher for your training data or your testing data? Why?

RMSE on training vs. testing

RMSE for testing:

rmse_test1 = np.sqrt(mean_squared_error(test['winpercent'], model.predict(test)))
print(f'RMSE Test 1: {rmse_test1}')

RMSE Test 1: 10.15009006066606

RMSE for training:

rmse_train1 = np.sqrt(mean_squared_error(train['winpercent'], model.predict(train)))
print(f'RMSE Train 1: {rmse_train1}')

RMSE Train 1: 10.117840760774037

CV 2

test_fold = 2
test = candy_rankings[candy_rankings['fold'] == test_fold]
train = candy_rankings[candy_rankings['fold'] != test_fold]
model = smf.ols('winpercent ~ chocolate + fruity + peanutyalmondy + crispedricewafer + hard + sugarpercent', data=train).fit()

rmse_test2 = np.sqrt(mean_squared_error(test['winpercent'], model.predict(test)))
rmse_train2 = np.sqrt(mean_squared_error(train['winpercent'], model.predict(train)))
print(f'RMSE Test 2: {rmse_test2}')
print(f'RMSE Train 2: {rmse_train2}')

RMSE Test 2: 10.432240639004073
RMSE Train 2: 10.027804484574576

CV 3

test_fold = 3
test = candy_rankings[candy_rankings['fold'] == test_fold]
train = candy_rankings[candy_rankings['fold'] != test_fold]
model = smf.ols('winpercent ~ chocolate + fruity + peanutyalmondy + crispedricewafer + hard + sugarpercent', data=train).fit()

rmse_test3 = np.sqrt(mean_squared_error(test['winpercent'], model.predict(test)))
rmse_train3 = np.sqrt(mean_squared_error(train['winpercent'], model.predict(train)))
print(f'RMSE Test 3: {rmse_test3}')
print(f'RMSE Train 3: {rmse_train3}')

RMSE Test 3: 11.95850312007085
RMSE Train 3: 9.801042089669558

CV 4

test_fold = 4
test = candy_rankings[candy_rankings['fold'] == test_fold]
train = candy_rankings[candy_rankings['fold'] != test_fold]
model = smf.ols('winpercent ~ chocolate + fruity + peanutyalmondy + crispedricewafer + hard + sugarpercent', data=train).fit()

rmse_test4 = np.sqrt(mean_squared_error(test['winpercent'], model.predict(test)))
rmse_train4 = np.sqrt(mean_squared_error(train['winpercent'], model.predict(train)))
print(f'RMSE Test 4: {rmse_test4}')
print(f'RMSE Train 4: {rmse_train4}')

RMSE Test 4: 12.39965858487449
RMSE Train 4: 9.60646325325732

CV 5

test_fold = 5
test = candy_rankings[candy_rankings['fold'] == test_fold]
train = candy_rankings[candy_rankings['fold'] != test_fold]
model = smf.ols('winpercent ~ chocolate + fruity + peanutyalmondy + crispedricewafer + hard + sugarpercent', data=train).fit()

rmse_test5 = np.sqrt(mean_squared_error(test['winpercent'], model.predict(test)))
rmse_train5 = np.sqrt(mean_squared_error(train['winpercent'], model.predict(train)))
print(f'RMSE Test 5: {rmse_test5}')
print(f'RMSE Train 5: {rmse_train5}')

RMSE Test 5: 10.01290509309602
RMSE Train 5: 10.13805597882432

Putting it altogether

Dataframe

rmse_candy = pd.DataFrame({
    'test_fold': np.arange(1, 6),
    'rmse_train': [rmse_train1, rmse_train2, rmse_train3, rmse_train4, rmse_train5],
    'rmse_test': [rmse_test1, rmse_test2, rmse_test3, rmse_test4, rmse_test5]
})

Visual

plt.figure(figsize=(8, 5))
sns.lineplot(data=rmse_candy, x='test_fold', y='rmse_test', marker='o', label='Test RMSE')
plt.xlabel('Fold')
plt.ylabel('RMSE')
plt.title('Test RMSE for each fold')
plt.legend()
plt.show()

How does RMSE compare to y?

winpercent summary stats:

count    85.000000
mean     50.316764
std      14.714357
min      22.445341
25%      39.141056
50%      47.829754
75%      59.863998
max      84.180290
Name: winpercent, dtype: float64

rmse_test summary stats:

count     5.000000
mean     10.990679
std       1.106390
min      10.012905
25%      10.150090
50%      10.432241
75%      11.958503
max      12.399659
Name: rmse_test, dtype: float64

`model_selection` in scikit-learn

The scikit-learn package provides functions that help you create pipelines when modeling.

from sklearn.model_selection import KFold

Cross Validation - Faster

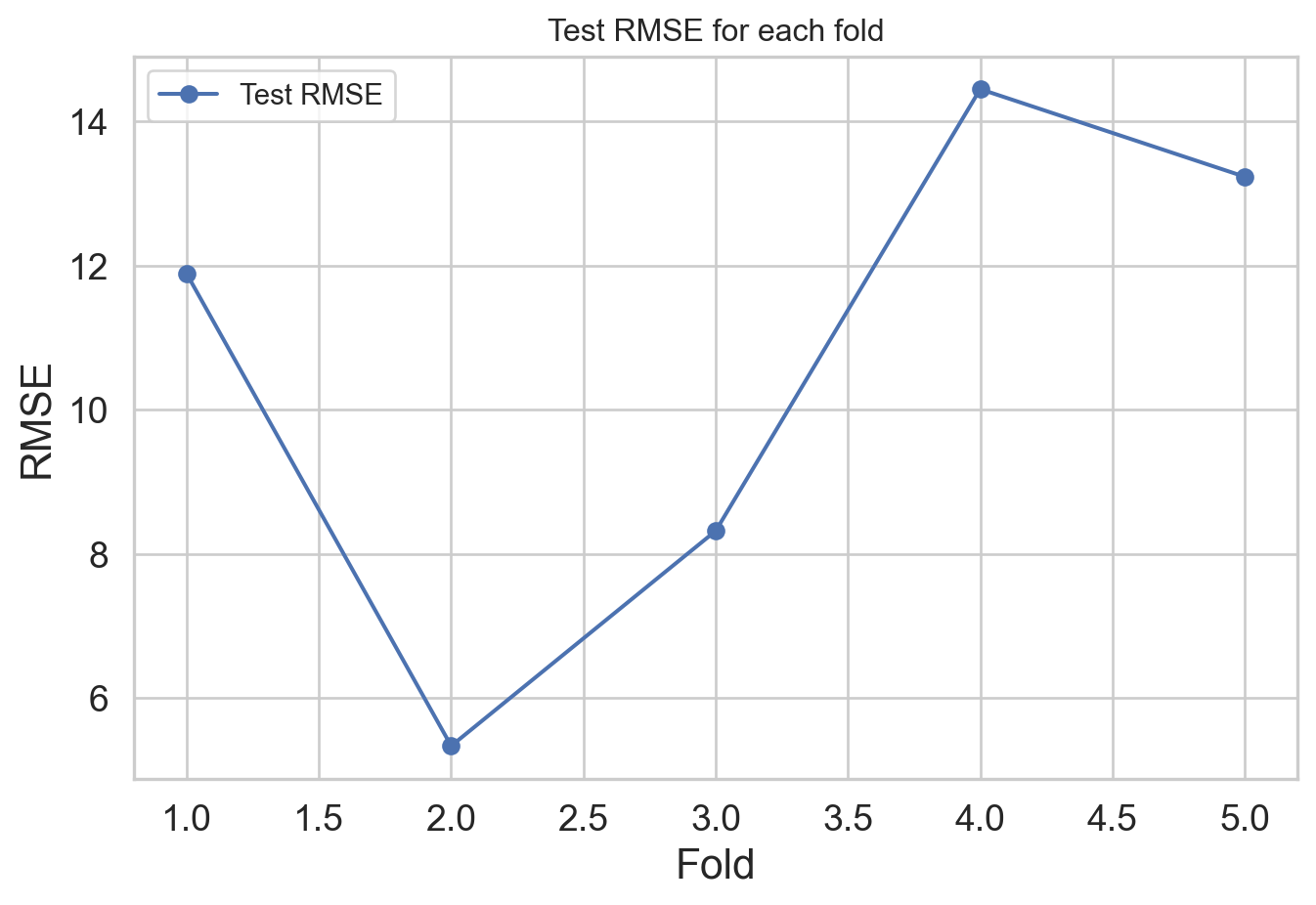
sklearn.model_selection.KFold: Partition data into k folds
Calculate RMSEs for each of the models on the testing set

Partition data into k folds

k = 5:

kf = KFold(n_splits=5, shuffle=True, random_state=102319)
folds = list(kf.split(candy_rankings))

Fit model on each of training set

rmses = []
for train_index, test_index in folds:
    train_data = candy_rankings.iloc[train_index]
    test_data = candy_rankings.iloc[test_index]
    model = smf.ols('winpercent ~ chocolate + fruity + peanutyalmondy + crispedricewafer + hard + sugarpercent', data=train_data).fit()
    rmse = np.sqrt(mean_squared_error(test_data['winpercent'], model.predict(test_data)))
    rmses.append(rmse)

Calculate RMSEs

Code

fold_ids = list(range(1, 6))
plt.figure(figsize=(8, 5))
plt.plot(fold_ids, rmses, marker='o', label='Test RMSE')
plt.xlabel('Fold')
plt.ylabel('RMSE')
plt.title('Test RMSE for each fold')
plt.legend()
plt.show()

rmse_summary = pd.Series(rmses).describe()
print(rmse_summary)

count     5.000000
mean     10.644100
std       3.751177
min       5.336119
25%       8.319019
50%      11.885830
75%      13.232239
max      14.447295
dtype: float64

Model validation

Setup

Data: Candy Rankings

Model validation

Overfitting

Model validation

Random sampling and reproducibility

Cross validation

Prepping your data for 5-fold CV

CV 1

RMSE on training vs. testing

RMSE on training vs. testing

CV 2

CV 3

CV 4

CV 5

Putting it altogether

How does RMSE compare to y?

model_selection in scikit-learn

Cross Validation - Faster

Partition data into k folds

Fit model on each of training set

Calculate RMSEs

`model_selection` in scikit-learn