import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
import statsmodels.formula.api as smf
sns.set_theme(style="whitegrid", rc={"figure.figsize": (10, 6), "axes.labelsize": 16, "xtick.labelsize": 14, "ytick.labelsize": 14})Logistic regression
Lecture 17
University of Arizona
INFO 511
Setup
Recap: Modeling Loans
What is the practical difference between a model with parallel and non-parallel lines?
What is the definition of R-squared?
Why do we choose models based on adjusted R-squared and not R-squared?
Predict interest rate…
from credit utilization and homeownership
Results: Ordinary least squares
=====================================================================
Model: OLS Adj. R-squared: 0.068
Dependent Variable: interest_rate AIC: 59859.3779
Date: 2026-02-23 11:17 BIC: 59888.2185
No. Observations: 9998 Log-Likelihood: -29926.
Df Model: 3 F-statistic: 243.7
Df Residuals: 9994 Prob (F-statistic): 1.25e-152
R-squared: 0.068 Scale: 23.309
---------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
---------------------------------------------------------------------
const 9.9250 0.1401 70.8498 0.0000 9.6504 10.1996
credit_util 5.3356 0.2074 25.7266 0.0000 4.9291 5.7421
homeownership_Mortgage 0.6956 0.1208 5.7590 0.0000 0.4588 0.9323
homeownership_Own 0.1283 0.1552 0.8266 0.4085 -0.1760 0.4326
---------------------------------------------------------------------
Omnibus: 1150.070 Durbin-Watson: 1.981
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1616.376
Skew: 0.900 Prob(JB): 0.000
Kurtosis: 3.800 Condition No.: 6
=====================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors
is correctly specified.Intercept
Results: Ordinary least squares
=====================================================================
Model: OLS Adj. R-squared: 0.068
Dependent Variable: interest_rate AIC: 59859.3779
Date: 2026-02-23 11:17 BIC: 59888.2185
No. Observations: 9998 Log-Likelihood: -29926.
Df Model: 3 F-statistic: 243.7
Df Residuals: 9994 Prob (F-statistic): 1.25e-152
R-squared: 0.068 Scale: 23.309
---------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
---------------------------------------------------------------------
const 9.9250 0.1401 70.8498 0.0000 9.6504 10.1996
credit_util 5.3356 0.2074 25.7266 0.0000 4.9291 5.7421
homeownership_Mortgage 0.6956 0.1208 5.7590 0.0000 0.4588 0.9323
homeownership_Own 0.1283 0.1552 0.8266 0.4085 -0.1760 0.4326
---------------------------------------------------------------------
Omnibus: 1150.070 Durbin-Watson: 1.981
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1616.376
Skew: 0.900 Prob(JB): 0.000
Kurtosis: 3.800 Condition No.: 6
=====================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors
is correctly specified.- Intercept: Loan applicants who rent and have 0 credit utilization are predicted to receive an interest rate of 9.93%, on average.
Slopes
Results: Ordinary least squares
=====================================================================
Model: OLS Adj. R-squared: 0.068
Dependent Variable: interest_rate AIC: 59859.3779
Date: 2026-02-23 11:17 BIC: 59888.2185
No. Observations: 9998 Log-Likelihood: -29926.
Df Model: 3 F-statistic: 243.7
Df Residuals: 9994 Prob (F-statistic): 1.25e-152
R-squared: 0.068 Scale: 23.309
---------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
---------------------------------------------------------------------
const 9.9250 0.1401 70.8498 0.0000 9.6504 10.1996
credit_util 5.3356 0.2074 25.7266 0.0000 4.9291 5.7421
homeownership_Mortgage 0.6956 0.1208 5.7590 0.0000 0.4588 0.9323
homeownership_Own 0.1283 0.1552 0.8266 0.4085 -0.1760 0.4326
---------------------------------------------------------------------
Omnibus: 1150.070 Durbin-Watson: 1.981
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1616.376
Skew: 0.900 Prob(JB): 0.000
Kurtosis: 3.800 Condition No.: 6
=====================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors
is correctly specified.All else held constant, for each additional percent credit utilization is higher, interest rate is predicted to be higher, on average, by 0.0534%.
All else held constant, the model predicts that loan applicants who have a mortgage for their home receive 0.696% higher interest rate than those who rent their home, on average.
All else held constant, the model predicts that loan applicants who own their home receive 0.128% higher interest rate than those who rent their home, on average.
Transformations
Predict log(interest rate)
Model
OLS Regression Results
==============================================================================
Dep. Variable: interest_rate R-squared: 0.020
Model: OLS Adj. R-squared: 0.020
Method: Least Squares F-statistic: 202.2
Date: Mon, 23 Feb 2026 Prob (F-statistic): 1.91e-45
Time: 11:17:47 Log-Likelihood: -4912.6
No. Observations: 9998 AIC: 9829.
Df Residuals: 9996 BIC: 9844.
Df Model: 1
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const 2.3947 0.005 467.428 0.000 2.385 2.405
credit_checks 0.0236 0.002 14.220 0.000 0.020 0.027
==============================================================================
Omnibus: 329.756 Durbin-Watson: 2.002
Prob(Omnibus): 0.000 Jarque-Bera (JB): 152.256
Skew: -0.010 Prob(JB): 8.67e-34
Kurtosis: 2.396 Cond. No. 4.17
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.\[ \widehat{log(interest~rate)} = 2.39 + 0.0236 \times credit~checks \]
Slope
OLS Regression Results
==============================================================================
Dep. Variable: interest_rate R-squared: 0.020
Model: OLS Adj. R-squared: 0.020
Method: Least Squares F-statistic: 202.2
Date: Mon, 23 Feb 2026 Prob (F-statistic): 1.91e-45
Time: 11:17:47 Log-Likelihood: -4912.6
No. Observations: 9998 AIC: 9829.
Df Residuals: 9996 BIC: 9844.
Df Model: 1
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const 2.3947 0.005 467.428 0.000 2.385 2.405
credit_checks 0.0236 0.002 14.220 0.000 0.020 0.027
==============================================================================
Omnibus: 329.756 Durbin-Watson: 2.002
Prob(Omnibus): 0.000 Jarque-Bera (JB): 152.256
Skew: -0.010 Prob(JB): 8.67e-34
Kurtosis: 2.396 Cond. No. 4.17
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.For each additional credit check, log of interest rate is predicted to be higher, on average, by 0.0236%.
Slope
\[ log(interest~rate_{x+1}) - log(interest~rate_{x}) = 0.0236 \]
\[ log(\frac{interest~rate_{x+1}}{interest~rate_{x}}) = 0.0236 \]
\[ e^{log(\frac{interest~rate_{x+1}}{interest~rate_{x}})} = e^{0.0236} \]
\[ \frac{interest~rate_{x+1}}{interest~rate_{x}} = 1.024 \]
For each additional credit check, interest rate is predicted to be higher, on average, by a factor of 1.024.
Logistic regression
What is logistic regression?
Similar to linear regression…. but
Modeling tool when our response is categorical
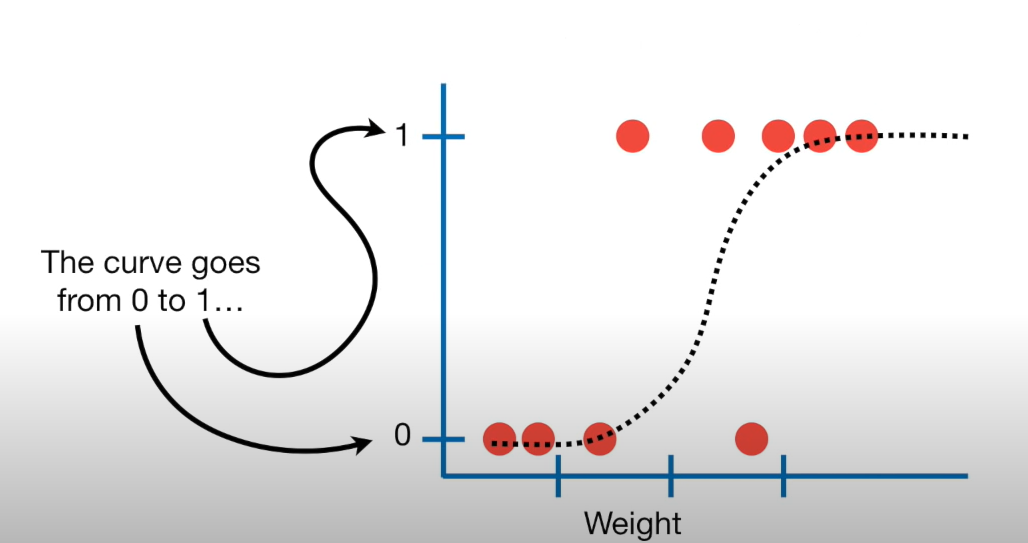
Modelling binary outcomes
Variables with binary outcomes follow the Bernouilli distribution:
\(y_i \sim Bern(p)\)
\(p\): Probability of success
\(1-p\): Probability of failure
We can’t model \(y\) directly, so instead we model \(p\)
Linear model
\[ p_i = \beta_o + \beta_1 \times X_1 + \cdots + \epsilon \]
But remember that \(p\) must be between 0 and 1
We need a link function that transforms the linear model to have an appropriate range
Logit link function
The logit function take values between 0 and 1 (probabilities) and maps them to values in the range negative infinity to positive infinity:
\[ logit(p) = log \bigg( \frac{p}{1 - p} \bigg) \]
This isn’t exactly what we need though…..
Recall, the goal is to take values between -\(\infty\) and \(\infty\) and map them to probabilities.
We need the opposite of the link function… or the inverse
Taking the inverse of the logit function will map arbitrary real values back to the range [0, 1]
Generalized linear model
- We model the logit (log-odds) of \(p\) :
\[ logit(p) = log \bigg( \frac{p}{1 - p} \bigg) = \beta_o + \beta_1 \times X1_i + \cdots + \epsilon \]
- Then take the inverse to obtain the predicted \(p\):
\[ p_i = \frac{e^{\beta_o + \beta_1 \times X1_i + \cdots + \epsilon}}{1 + e^{\beta_o + \beta_1 \times X1_i + \cdots + \epsilon}} \]
A logistic model visualized
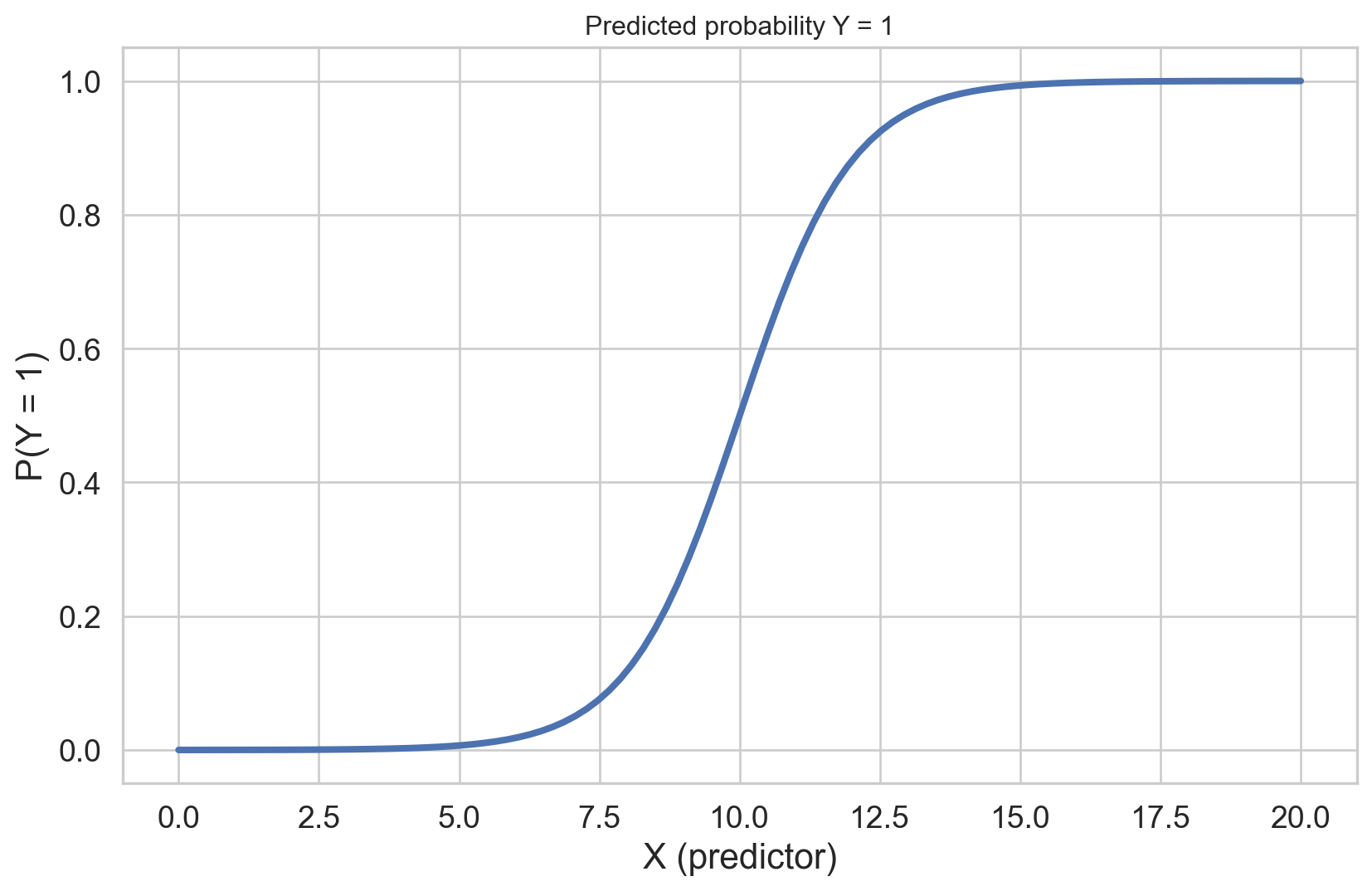
Takeaways
Generalized linear models allow us to fit models to predict non-continuous outcomes
Predicting binary outcomes requires modeling the log-odds of success, where p = probability of success
