Linear regression

Lecture 15

Dr. Greg Chism

University of Arizona
INFO 511 - Fall 2024

Setup

import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
import numpy as np
from great_tables import GT, style, loc, exibble

# Setting the theme for plots
sns.set_theme(style="whitegrid", font_scale=1.2)

Goals

  • What is a model?
  • Why do we model?
  • What is correlation?

Prediction / classification

Let’s drive a Tesla!

Semi or garage?

i love how Tesla thinks the wall in my garage is a semi. 😅

Semi or garage?

New owner here. Just parked in my garage. Tesla thinks I crashed onto a semi.

Car or trash?

Tesla calls Mercedes trash

Description

Leisure, commute, physical activity and BP

Relation Between Leisure Time, Commuting, and Occupational Physical Activity With Blood Pressure in 125,402 Adults: The Lifelines Cohort

Byambasukh, Oyuntugs, Harold Snieder, and Eva Corpeleijn. “Relation between leisure time, commuting, and occupational physical activity with blood pressure in 125 402 adults: the lifelines cohort.” Journal of the American Heart Association 9.4 (2020): e014313.

Leisure, commute, physical activity and BP

Background: Whether all domains of daily‐life moderate‐to‐vigorous physical activity (MVPA) are associated with lower blood pressure (BP) and how this association depends on age and body mass index remains unclear.

Methods and Results: In the population‐based Lifelines cohort (N=125,402), MVPA was assessed by the Short Questionnaire to Assess Health‐Enhancing Physical Activity, a validated questionnaire in different domains such as commuting, leisure‐time, and occupational PA. BP was assessed using the last 3 of 10 measurements after 10 minutes’ rest in the supine position. Hypertension was defined as systolic BP ≥140 mm Hg and/or diastolic BP ≥90 mm Hg and/or use of antihypertensives. In regression analysis, higher commuting and leisure‐time but not occupational MVPA related to lower BP and lower hypertension risk. Commuting‐and‐leisure‐time MVPA was associated with BP in a dose‐dependent manner. β Coefficients (95% CI) from linear regression analyses were −1.64 (−2.03 to −1.24), −2.29 (−2.68 to −1.90), and finally −2.90 (−3.29 to −2.50) mm Hg systolic BP for the low, middle, and highest tertile of MVPA compared with “No MVPA” as the reference group after adjusting for age, sex, education, smoking and alcohol use. Further adjustment for body mass index attenuated the associations by 30% to 50%, but more MVPA remained significantly associated with lower BP and lower risk of hypertension. This association was age dependent. β Coefficients (95% CI) for the highest tertiles of commuting‐and‐leisure‐time MVPA were −1.67 (−2.20 to −1.15), −3.39 (−3.94 to −2.82) and −4.64 (−6.15 to −3.14) mm Hg systolic BP in adults <40, 40 to 60, and >60 years, respectively.

Conclusions: Higher commuting and leisure‐time but not occupational MVPA were significantly associated with lower BP and lower hypertension risk at all ages, but these associations were stronger in older adults.

Modeling

Modeling cars

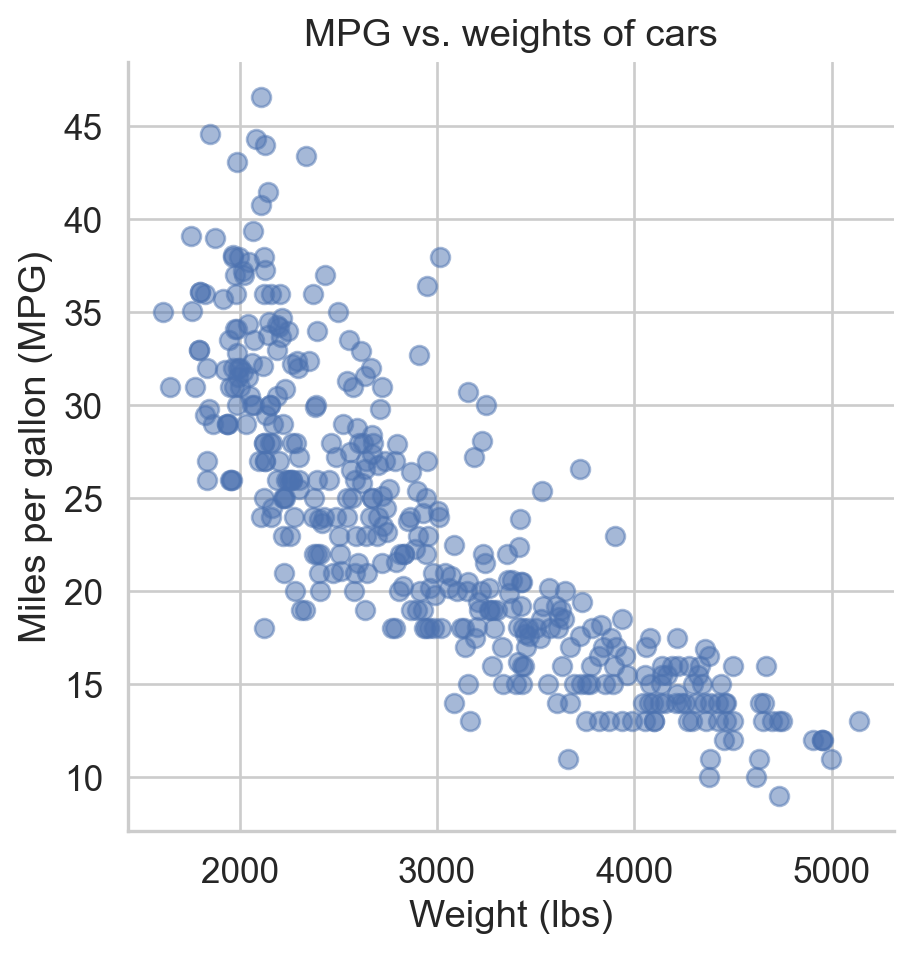
  • What is the relationship between cars’ weights and their mileage?
  • What is your best guess for a car’s MPG that weighs 3,500 pounds?

Modelling cars

Describe: What is the relationship between cars’ weights and their mileage?

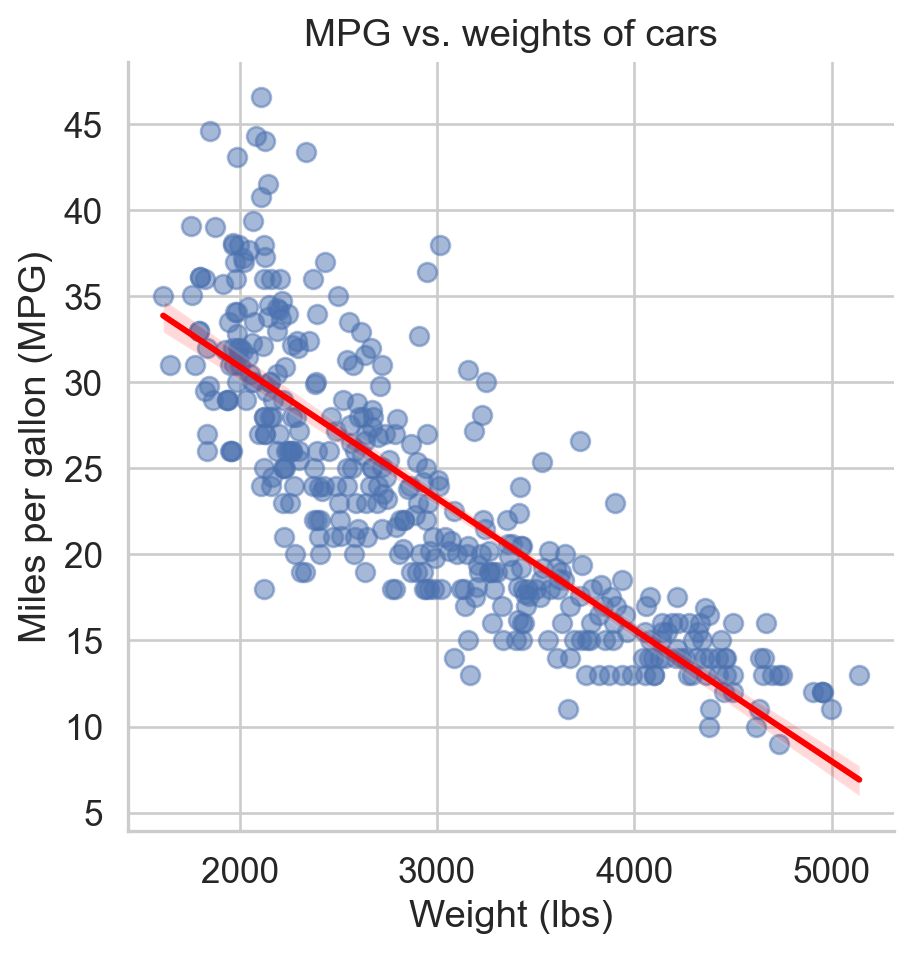
Modelling cars

Predict: What is your best guess for a car’s MPG that weighs 3,500 pounds?

Modelling

  • Use models to explain the relationship between variables and to make predictions
  • For now we will focus on linear models (but there are many many other types of models too!)

Modelling vocabulary

  • Predictor (explanatory variable)
  • Outcome (response variable)
  • Regression line
    • Slope
    • Intercept
  • Correlation

Predictor (explanatory variable)

mpg weight
18.0 3504
15.0 3693
18.0 3436
16.0 3433
17.0 3449
15.0 4341
... ...

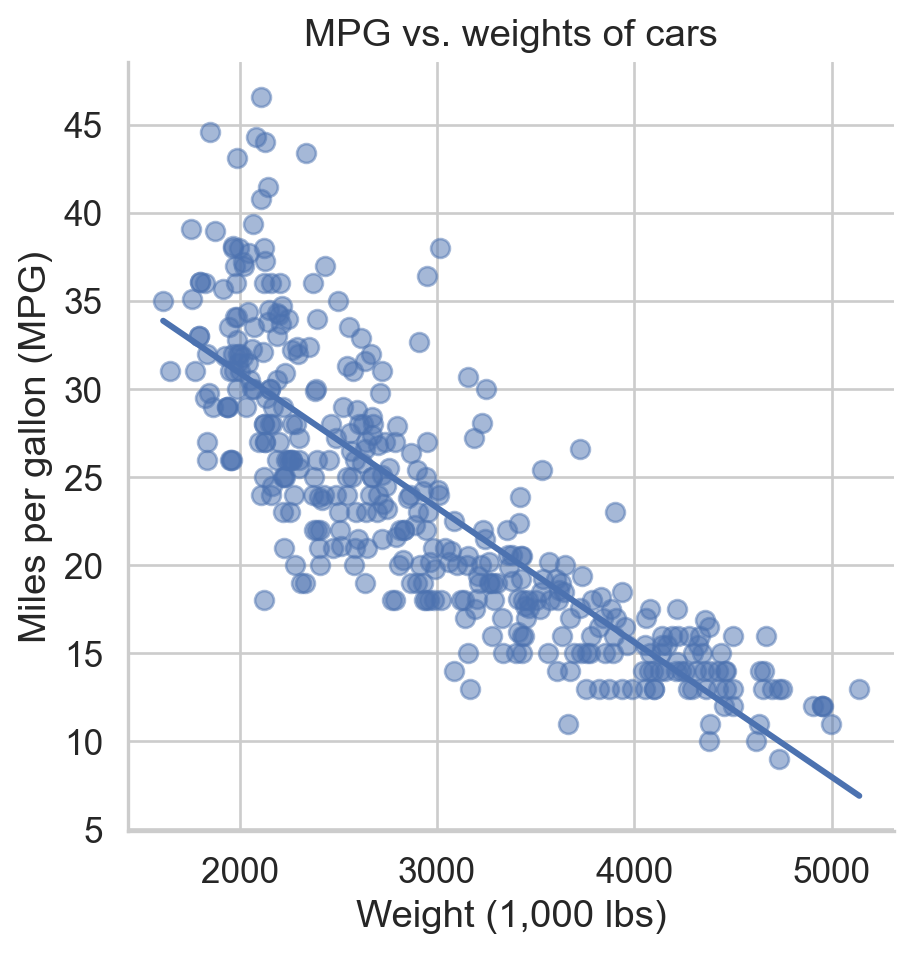
Outcome (response variable)

mpg weight
18.0 3504
15.0 3693
18.0 3436
16.0 3433
17.0 3449
15.0 4341
... ...

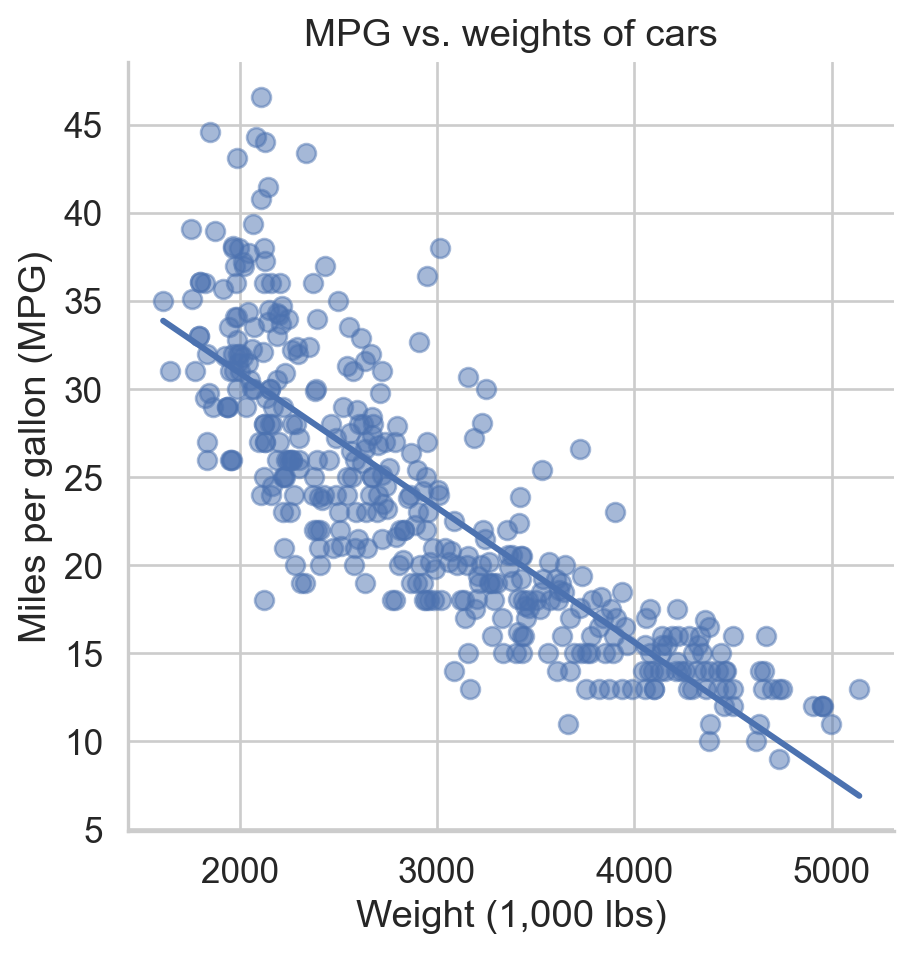
Regression line

Regression line: slope

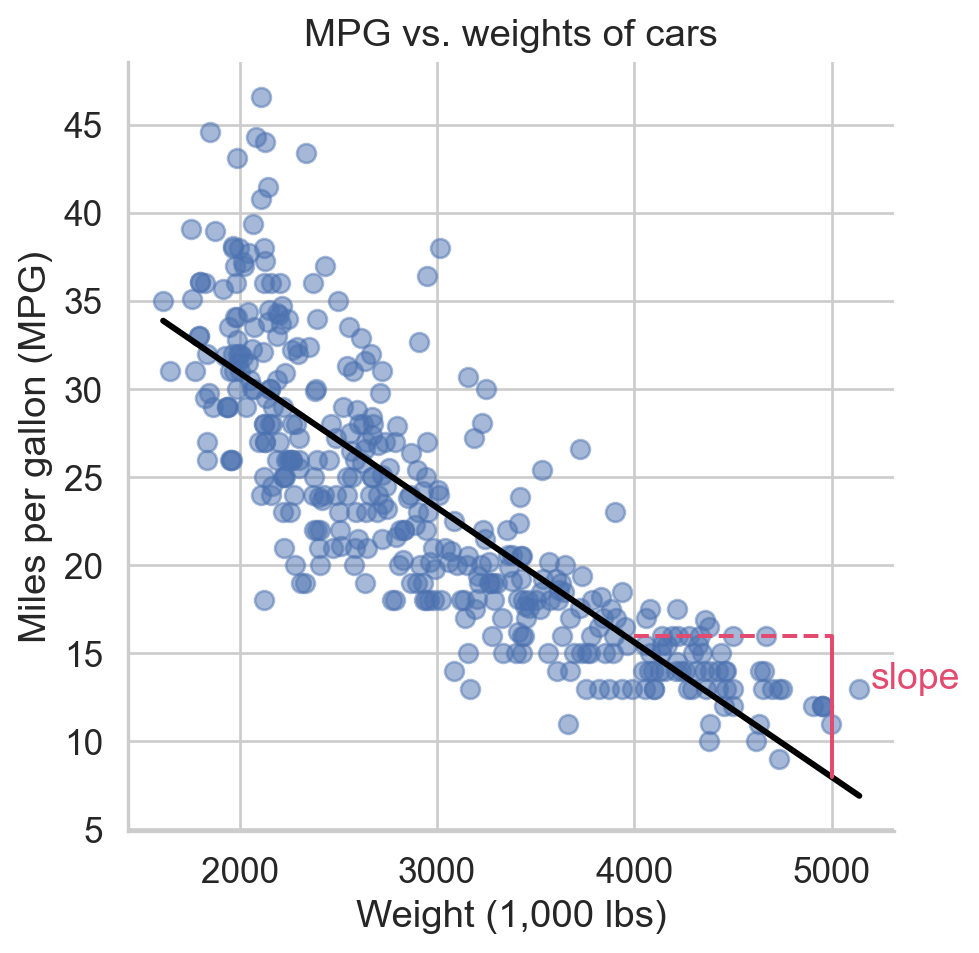
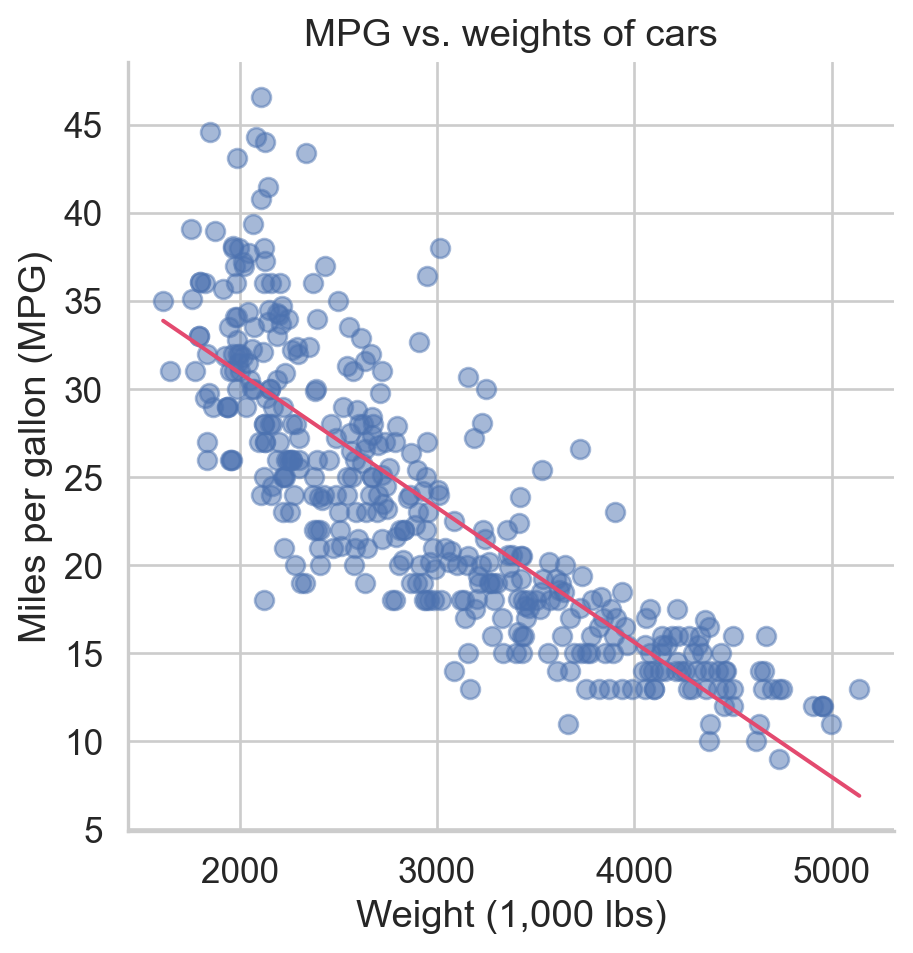
Regression line: intercept

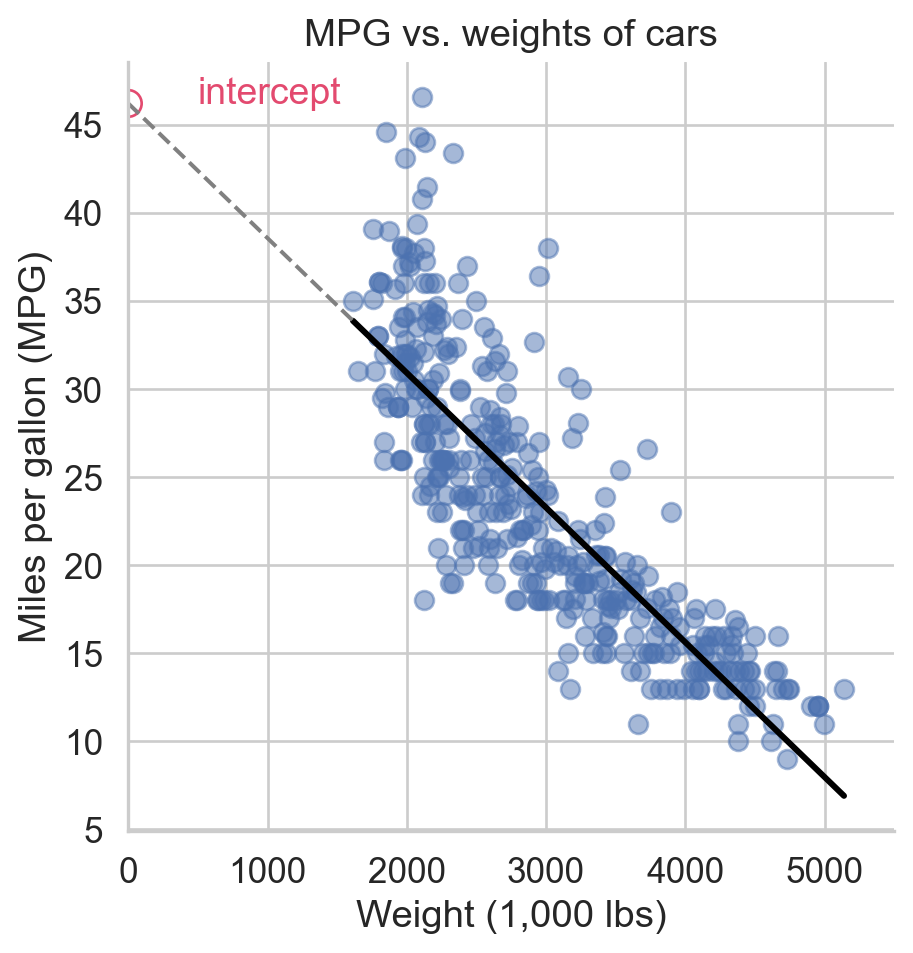
Correlation

Correlation coefficient: -0.83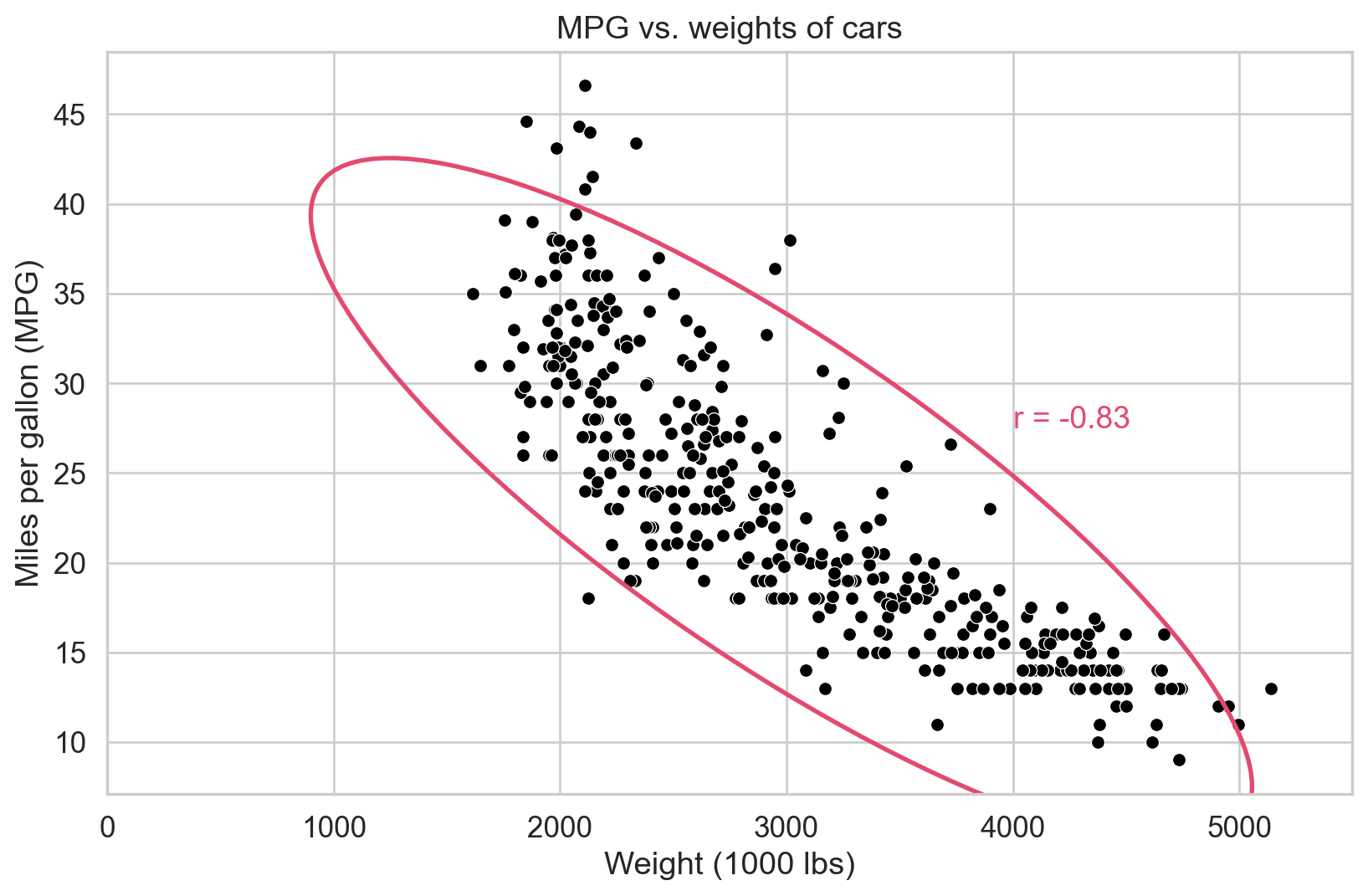

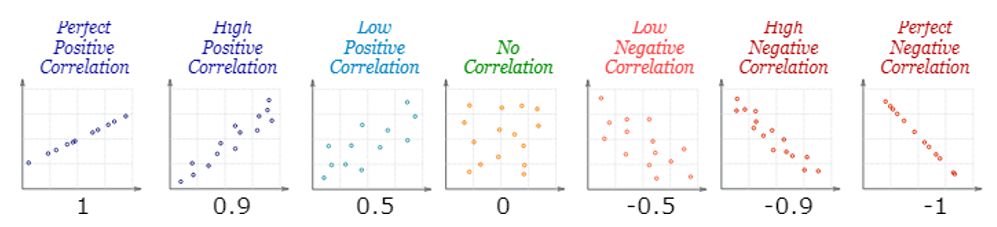
Correlation

  • Ranges between -1 and 1.
  • Same sign as the slope.

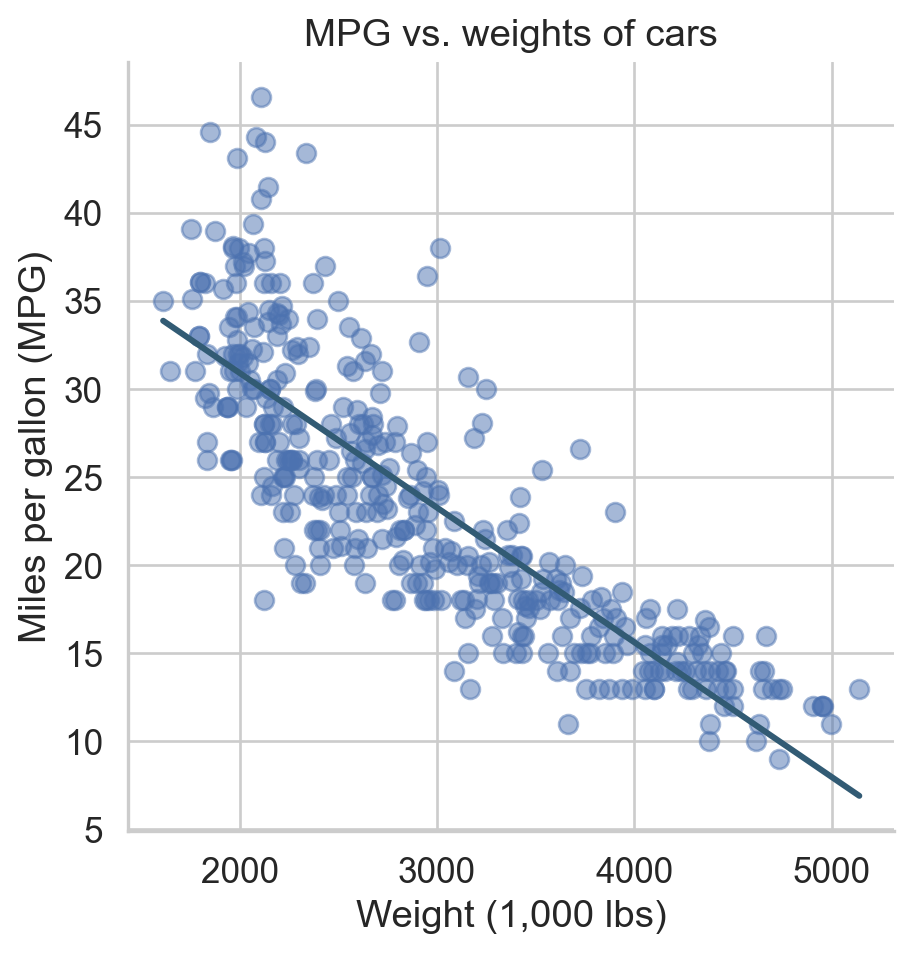
Visualizing the model

Code 
sns.lmplot(x="weight", y="mpg", data=mtcars, ci=None, scatter_kws={"s": 50, "alpha": 0.5}, line_kws={"color": "#325b74"})
plt.xlabel("Weight (1,000 lbs)")
plt.ylabel("Miles per gallon (MPG)")
plt.title("MPG vs. weights of cars")
plt.show()

Linear regression with a single predictor

Data prep

  • Rename Rotten Tomatoes columns as critics and audience
  • Rename the dataset as movie_scores
fandango = pd.read_csv("data/fandango.csv")
movie_scores = fandango.rename(columns={"rt_norm": "critics", "rt_user_norm": "audience"})

Data overview

print(movie_scores[["critics", "audience"]].head())
   critics  audience
0     3.70       4.3
1     4.25       4.0
2     4.00       4.5
3     0.90       4.2
4     0.70       1.4

Data visualization

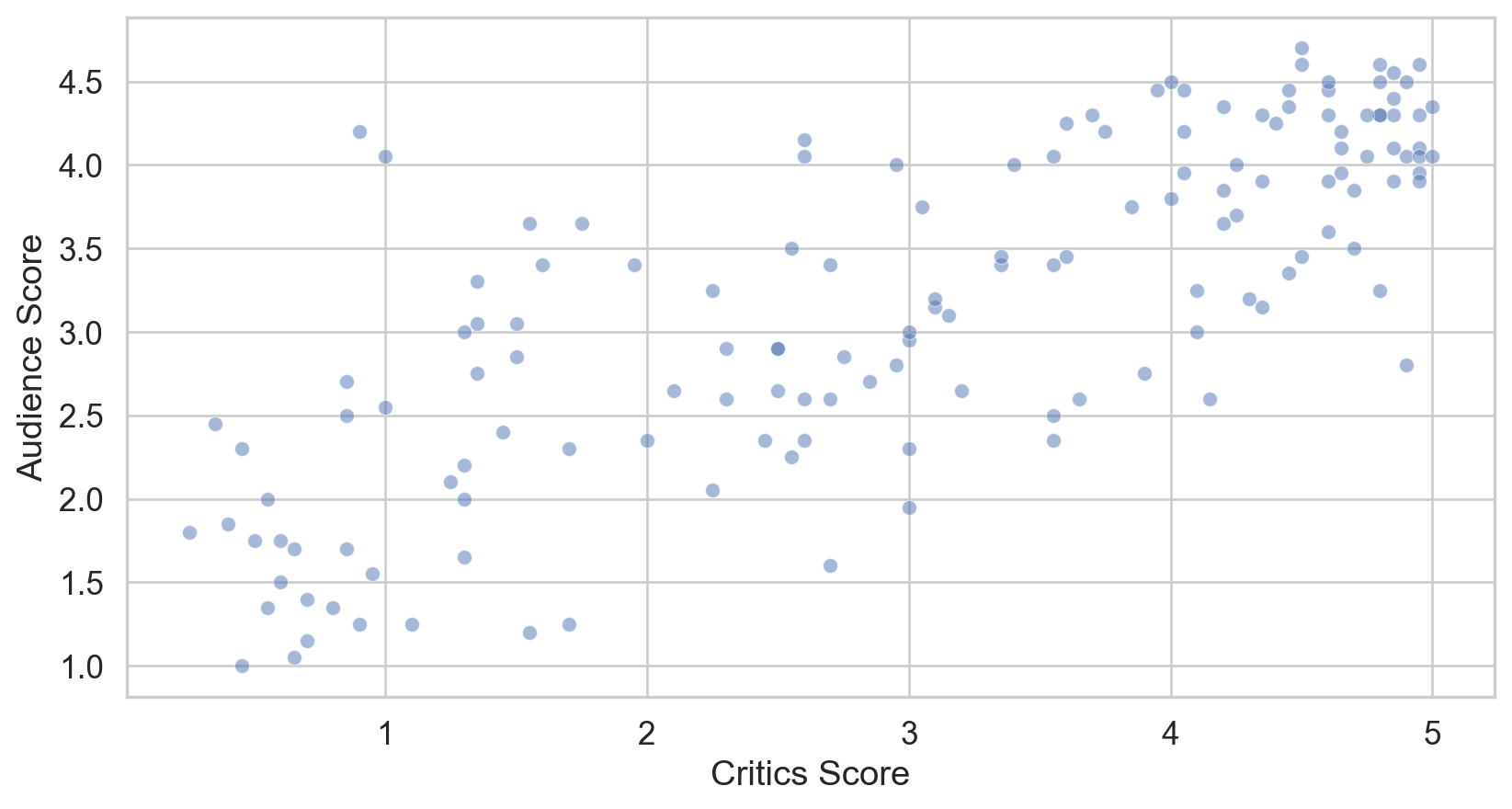
Regression model

A regression model is a function that describes the relationship between the outcome, \(Y\), and the predictor, \(X\).

\[\begin{aligned} Y &= \color{black}{\textbf{Model}} + \text{Error} \\[8pt] &= \color{black}{\mathbf{f(X)}} + \epsilon \\[8pt] &= \color{black}{\boldsymbol{\mu_{Y|X}}} + \epsilon \end{aligned}\]

Regression model

\[ \begin{aligned} Y &= \color{#325b74}{\textbf{Model}} + \text{Error} \\[8pt] &= \color{#325b74}{\mathbf{f(X)}} + \epsilon \\[8pt] &= \color{#325b74}{\boldsymbol{\mu_{Y|X}}} + \epsilon \end{aligned} \]

Simple linear regression

Use simple linear regression to model the relationship between a quantitative outcome (\(Y\)) and a single quantitative predictor (\(X\)): \[\Large{Y = \beta_0 + \beta_1 X + \epsilon}\]

  • \(\beta_1\): True slope of the relationship between \(X\) and \(Y\)
  • \(\beta_0\): True intercept of the relationship between \(X\) and \(Y\)
  • \(\epsilon\): Error (residual)

Simple linear regression

\[\Large{\hat{Y} = b_0 + b_1 X}\]

  • \(b_1\): Estimated slope of the relationship between \(X\) and \(Y\)
  • \(b_0\): Estimated intercept of the relationship between \(X\) and \(Y\)
  • No error term!

Residuals

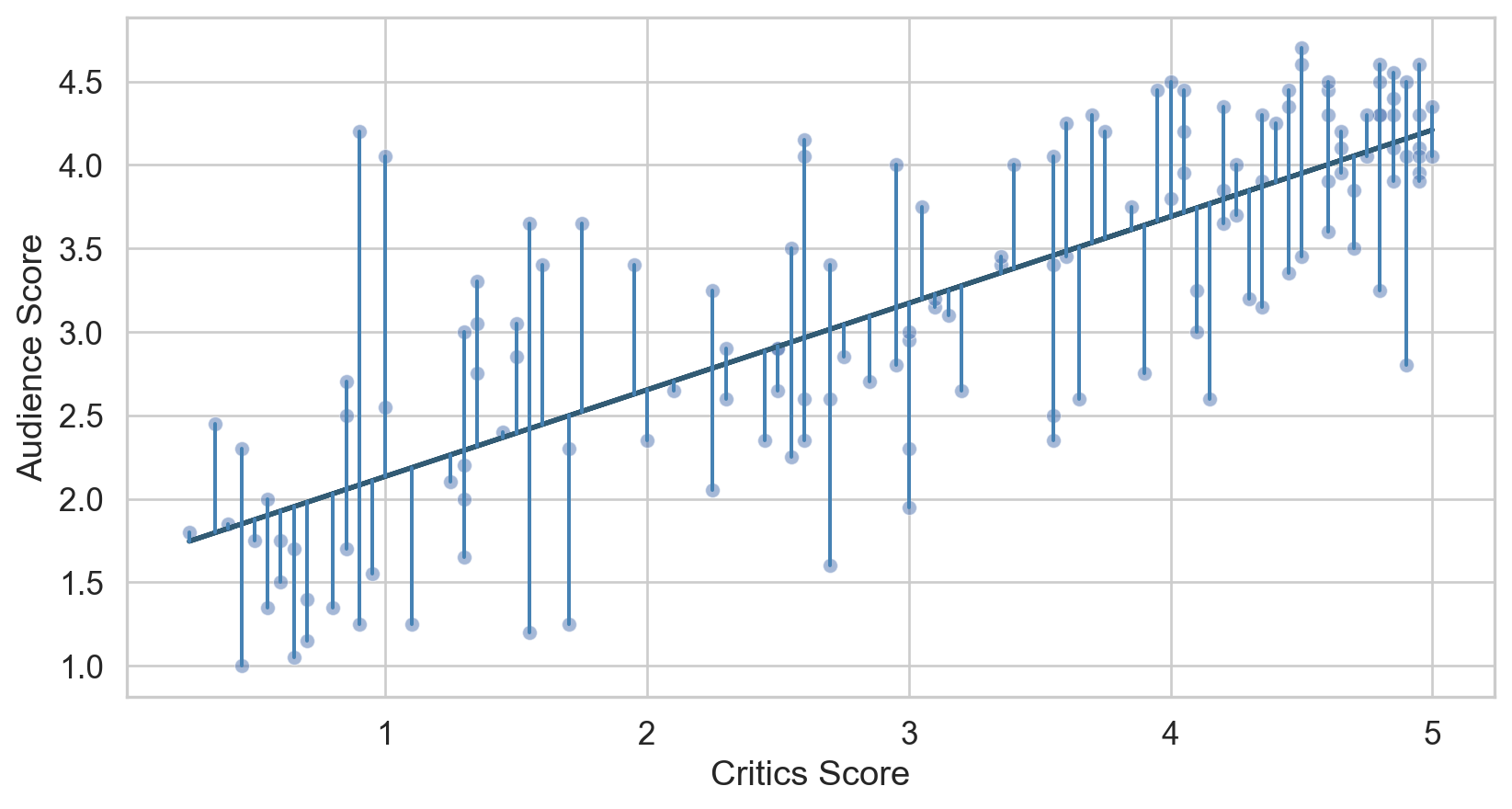
\[\text{residual} = \text{observed} - \text{predicted} = y - \hat{y}\]

Least squares line

  • The residual for the \(i^{th}\) observation is

\[e_i = \text{observed} - \text{predicted} = y_i - \hat{y}_i\]

  • The sum of squared residuals is

\[e^2_1 + e^2_2 + \dots + e^2_n\]

  • The least squares line is the one that minimizes the sum of squared residuals

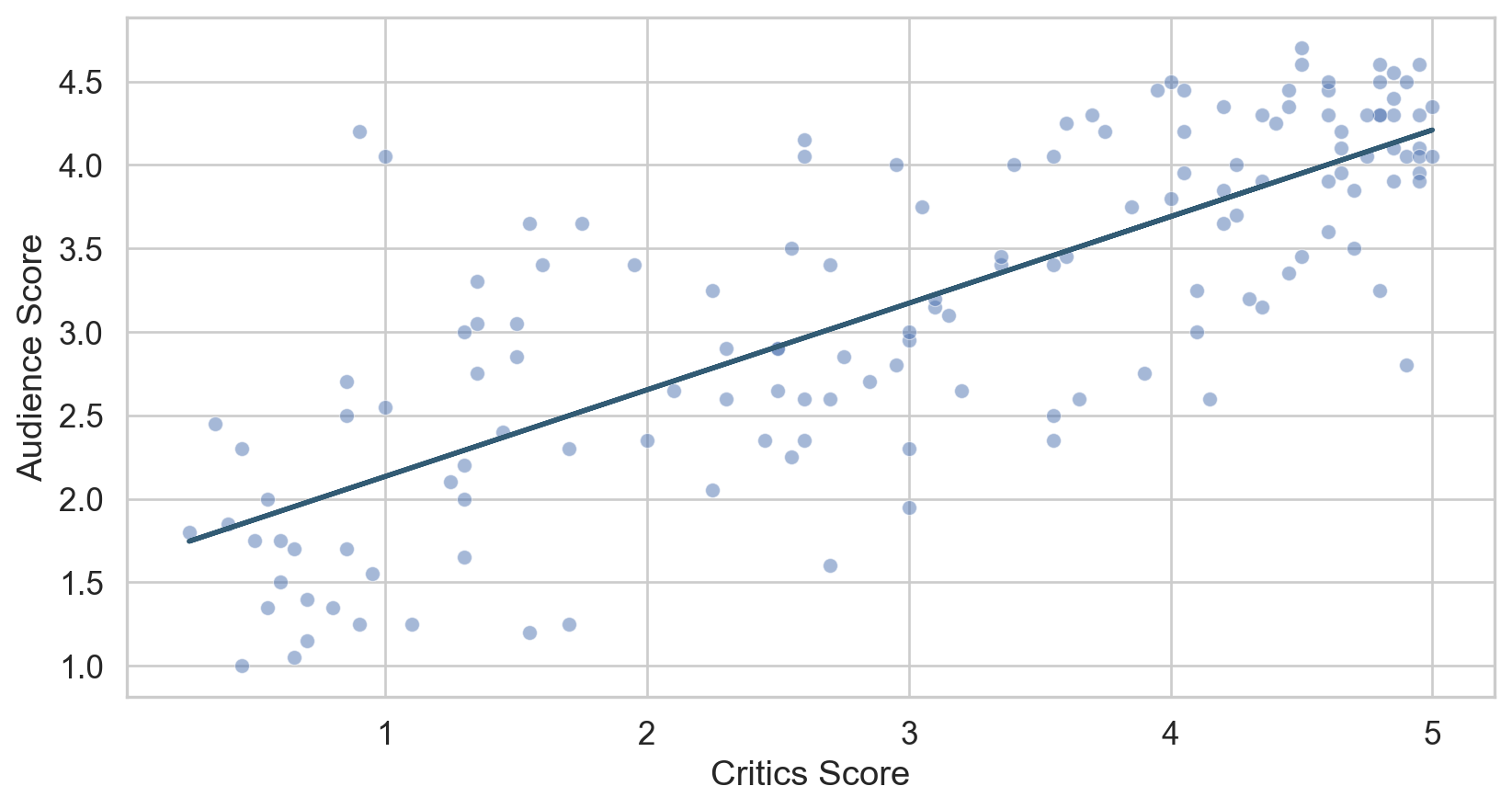
Least squares line

slope, intercept = model.coef_[0], model.intercept_
print(f"Slope: {slope:.2f}, Intercept: {intercept:.2f}")
Slope: 0.52, Intercept: 1.62

Slope and intercept

Properties of least squares regression

  • The regression line goes through the center of mass point (the coordinates corresponding to average \(X\) and average \(Y\)): \(b_0 = \bar{Y} - b_1~\bar{X}\)

  • Slope has the same sign as the correlation coefficient: \(b_1 = r \frac{s_Y}{s_X}\)

  • Sum of the residuals is zero: \(\sum_{i = 1}^n \epsilon_i = 0\)

  • Residuals and \(X\) values are uncorrelated

Interpreting slope & intercept

\[\widehat{\text{audience}} = 32.3 + 0.519 \times \text{critics}\]

  • Slope: For every one point increase in the critics score, we expect the audience score to be higher by 0.519 points, on average.
  • Intercept: If the critics score is 0 points, we expect the audience score to be 32.3 points.

Is the intercept meaningful?

✅ The intercept is meaningful in context of the data if

  • the predictor can feasibly take values equal to or near zero or
  • the predictor has values near zero in the observed data

🛑 Otherwise, it might not be meaningful!

Application exercise

Application exercise: ae-10-modeling-fish

  • Go back to your project called ae.
  • If there are any uncommitted files, commit them, and push.

🔗 datasciaz.netlify.app