Sampling distributions + inference

Lecture 14

Dr. Greg Chism

University of Arizona
INFO 511 - Fall 2024

Setup

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats 
import seaborn as sns

np.random.seed(1)

Sample Statistics and Sampling Distributions

Variability of sample statistics

We’ve seen that each sample from the population yields a slightly different sample statistic (sample mean, sample proportion, etc.)
Previously we’ve quantified this value via simulation
Today we talk about some of the theory underlying sampling distributions, particularly as they relate to sample means.

Statistical inference

Statistical inference is the act of generalizing from a sample in order to make conclusions regarding a population.
We are interested in population parameters, which we do not observe. Instead, we must calculate statistics from our sample in order to learn about them.
As part of this process, we must quantify the degree of uncertainty in our sample statistic.

Sampling distribution of the mean

Suppose we’re interested in the mean resting heart rate of students at U of A, and are able to do the following:

Take a random sample of size \(n\) from this population, and calculate the mean resting heart rate in this sample, \(\bar{X}_1\)
Put the sample back, take a second random sample of size \(n\), and calculate the mean resting heart rate from this new sample, \(\bar{X}_2\)
Put the sample back, take a third random sample of size \(n\), and calculate the mean resting heart rate from this sample, too…

…and so on.

Sampling distribution of the mean

After repeating this many times, we have a data set that has the sample means from the population: \(\bar{X}_1\), \(\bar{X}_2\), \(\cdots\), \(\bar{X}_K\) (assuming we took \(K\) total samples).

Can we say anything about the distribution of these sample means (that is, the sampling distribution of the mean?)

(Keep in mind, we don’t know what the underlying distribution of mean resting heart rate of U of A students looks like!)

Central Limit Theorem

😱

The Central Limit Theorem

A quick caveat…

For now, let’s assume we know the underlying standard deviation, \(\sigma\), from our distribution

The Central Limit Theorem

For a population with a well-defined mean \(\mu\) and standard deviation \(\sigma\), these three properties hold for the distribution of sample mean \(\bar{X}\), assuming certain conditions hold:

The mean of the sampling distribution of the mean is identical to the population mean \(\mu\).
The standard deviation of the distribution of the sample means is \(\sigma/\sqrt{n}\).

This is called the standard error (SE) of the mean.

For \(n\) large enough, the shape of the sampling distribution of means is approximately normally distributed.

The normal (Gaussian) distribution

The normal distribution is unimodal and symmetric and is described by its density function:

If a random variable \(X\) follows the normal distribution, then \[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{1}{2}\frac{(x - \mu)^2}{\sigma^2} \right\}\] where \(\mu\) is the mean and \(\sigma^2\) is the variance \((\sigma \text{ is the standard deviation})\)

Warning

We often write \(N(\mu, \sigma)\) to describe this distribution.

The normal distribution (graphically)

Wait, any distribution?

The central limit theorem tells us that sample means are normally distributed, if we have enough data and certain assumptions hold.

This is true even if our original variables are not normally distributed.

Click here to see an interactive demonstration of this idea.

Conditions for CLT

We need to check two conditions for CLT to hold: independence, sample size/distribution.

✅ Independence: The sampled observations must be independent. This is difficult to check, but the following are useful guidelines:

the sample must be randomly taken
if sampling without replacement, sample size must be less than 10% of the population size

If samples are independent, then by definition one sample’s value does not “influence” another sample’s value.

Conditions for CLT

✅ Sample size / distribution:

if data are numerical, usually n > 30 is considered a large enough sample for the CLT to apply
if we know for sure that the underlying data are normally distributed, then the distribution of sample means will also be exactly normal, regardless of the sample size
if data are categorical, at least 10 successes and 10 failures.

Let’s run our own simulation

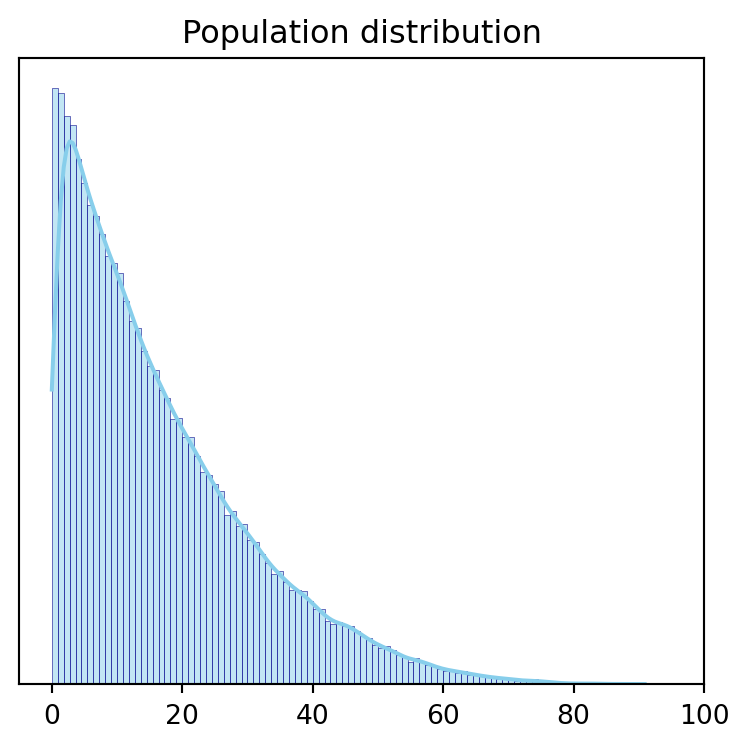
Underlying population (not observed in real life!)

rs_pop = pd.DataFrame({'x': np.random.beta(a=1, b=5, size=100000) * 100})

The true population parameters

(16.6681176684249, 14.070251294281247)

Sampling from the population - 1

np.random.seed(1)
samp_1 = rs_pop.sample(n=50)
samp_1_mean = samp_1['x'].mean()

samp_1_mean

15.459323508748778

Sampling from the population - 2

np.random.seed(2)
samp_2 = rs_pop.sample(n=50)
samp_2_mean = samp_2['x'].mean()

samp_2_mean

16.54881766128449

Sampling from the population - 3

np.random.seed(3)
samp_3 = rs_pop.sample(n=50)
samp_3_mean = samp_3['x'].mean()

samp_3_mean

18.232335628488613

keep repeating…

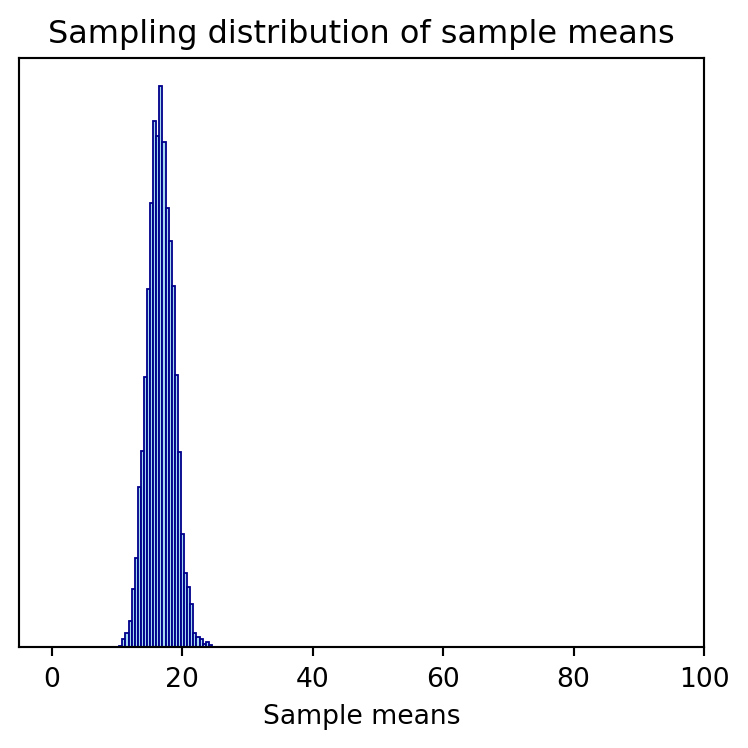
Sampling distribution

np.random.seed(92620)
sampling_means = [rs_pop.sample(n=50, replace=True)['x'].mean() for _ in range(5000)]

sampling_df = pd.DataFrame({'xbar': sampling_means})

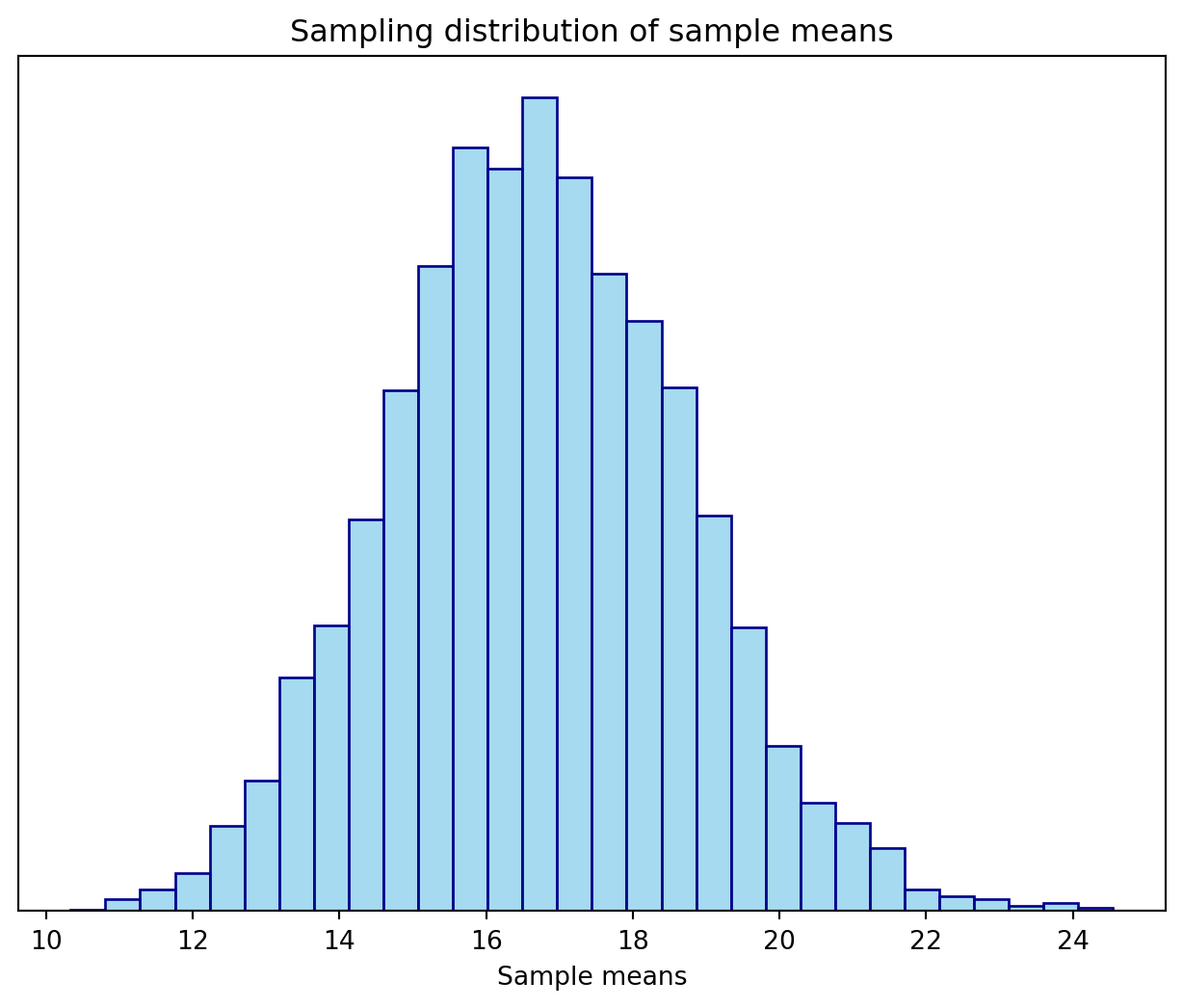
The sample statistics

(16.71372258467488, 1.9996839510659443)

Compare the shapes, centers, and spreads of these distributions:

The true population

The sample statistics

Recap

If certain assumptions are satisfied, regardless of the shape of the population distribution, the sampling distribution of the mean follows an approximately normal distribution.
The center of the sampling distribution is at the center of the population distribution.
The sampling distribution is less variable than the population distribution (and we can quantify by how much).

What is the standard error, and how are the standard error and sample size related? What does that say about how the spread of the sampling distribution changes as \(n\) increases?

Why do we care?

Knowing the distribution of the sample statistic \(\bar{X}\) can help us

Estimate a population parameter as point estimate \(\boldsymbol{\pm}\) margin of error

The margin of error is comprised of a measure of how confident we want to be and how variable the sample statistic is

Test for a population parameter by evaluating how likely it is to obtain to observed sample statistic when assuming that the null hypothesis is true
- This probability will depend on how variable the sampling distribution is

Inference based on the CLT

If necessary conditions are met, we can also use inference methods based on the CLT. Suppose we know the true population standard deviation, \(\sigma\).

Then the CLT tells us that \(\bar{X}\) approximately has the distribution \(N\left(\mu, \sigma/\sqrt{n}\right)\).

That is,

\[Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim N(0, 1)\]

What if \(\sigma\) isn’t known?

T distribution

In practice, we never know the true value of \(\sigma\), and so we estimate it from our data with \(s\).

We can make the following test statistic for testing a single sample’s population mean, which has a t-distribution with n-1 degrees of freedom:

\[ T = \frac{\bar{X} - \mu}{s/\sqrt{n}} \sim t_{n-1}\]

T distribution

The t-distribution is also unimodal and symmetric, and is centered at 0
It has thicker tails than the normal distribution
- This is to make up for additional variability introduced by using \(s\) instead of \(\sigma\) in calculation of the SE
It is defined by the degrees of freedom

T vs Z distributions

T distribution

Finding probabilities under the t curve:

# P(t < -1.96) for df = 9
p_less = stats.t.cdf(-1.96, df=9)
p_less

0.04082220273020832

# P(t > -1.96) for df = 9
p_greater = stats.t.sf(-1.96, df=9)
p_greater

0.9591777972697917

Finding cutoff values under the t curve:

# Find Q1 (25th percentile) for df = 9
q1 = stats.t.ppf(0.25, df=9)
q1

-0.7027221467513188

# Find Q3 (75th percentile) for df = 9
q3 = stats.t.ppf(0.75, df=9)
q3

0.7027221467513188

Confidence interval for a mean

Warning

General form of the confidence interval

\[point~estimate \pm critical~value \times SE\]

Warning

Confidence interval for the mean

\[\bar{x} \pm t^*_{n-1} \times \frac{s}{\sqrt{n}}\]

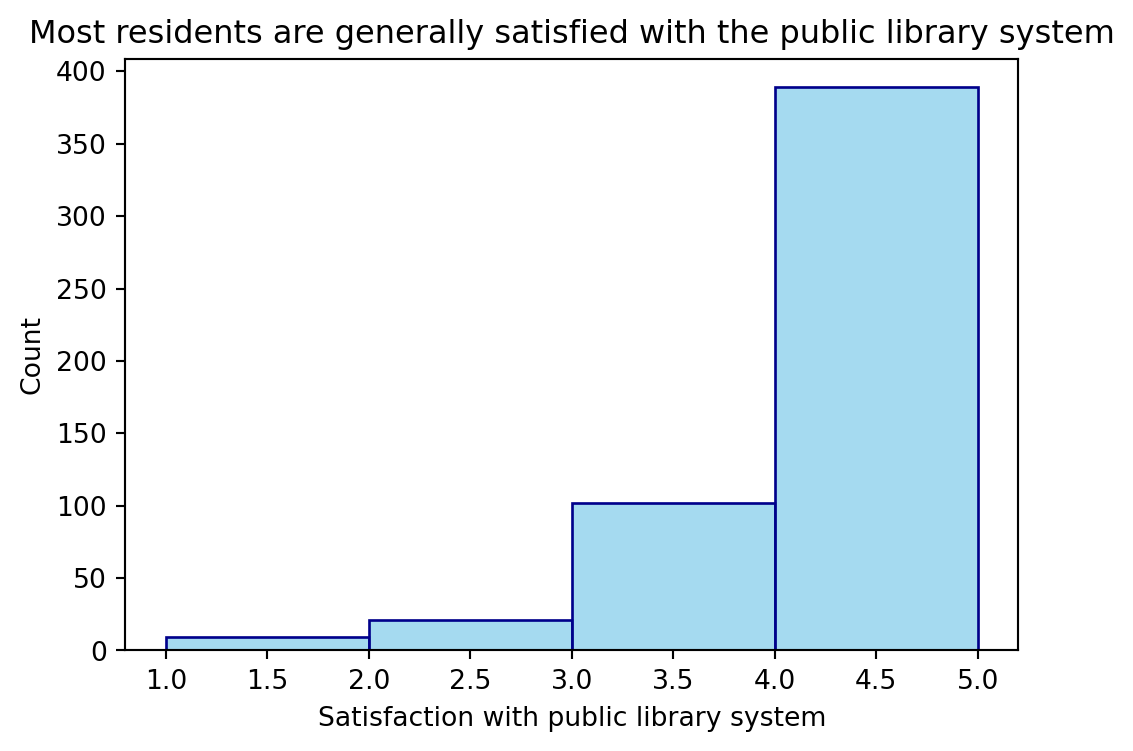
Durham NC Resident Satisfaction

durham_survey contains resident responses to a survey given by the City of Durham in 2018. These are a randomly selected, representative sample of Durham residents.

Questions were rated 1 - 5, with 1 being “highly dissatisfied” and 5 being “highly satisfied.”

Exploratory Data Analysis

durham = pd.read_csv("data/durham_survey.csv")
durham_filtered = durham[durham['quality_library'] != 9]

summary_stats = durham_filtered['quality_library'].agg(['mean', 'median', 'std', 'count']).rename({
    'mean': 'x_bar',
    'median': 'med',
    'std': 'sd',
    'count': 'n'
})
print(summary_stats)

x_bar      3.96929
med        4.00000
sd         0.90033
n        521.00000
Name: quality_library, dtype: float64

Calculate 95% confidence interval

\[\bar{x} \pm t^*_{n-1} \times \frac{s}{\sqrt{n}}\]

point_est = summary_stats['x_bar'] # Point estimate
se = summary_stats['sd'] / (summary_stats['n'] ** 0.5) # SE
df = summary_stats['n'] - 1 # Degrees of freedom

t_star = stats.t.ppf(0.975, df) # Critical value

# Confidence interval
CI = point_est + np.array([-1, 1]) * t_star * se
CI_rounded = np.round(CI, 2)
CI_rounded

array([3.89, 4.05])

Interpret 95% confidence interval

The 95% confidence interval is 3.89 to 4.05.

Interpret this interval in context of the data.

We are 95% confident that the true mean rating for Durham residents’ satisfaction with the library system is between 3.89 and 4.05.