Hypothesis testing

Lecture 13

Dr. Greg Chism

University of Arizona
INFO 511 - Fall 2024

Setup

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
import random

sns.set(font_scale=2)
sns.set_theme(style = "whitegrid")

Hypothesis testing

How can we answer questions using statistics?

Statistical hypothesis testing is the procedure that assesses evidence provided by the data in favor of or against some claim about the population (often about a population parameter or potential associations)

The hypothesis testing framework

Ei incumbit probatio qui dicit, non qui negat

The hypothesis testing framework

Start with two hypotheses about the population: the null hypothesis and the alternative hypothesis.
Choose a (representative) sample, collect data, and analyze the data.
Figure out how likely it is to see data like what we observed, IF the null hypothesis were in fact true.
If our data would have been extremely unlikely if the null claim were true, then we reject it and deem the alternative claim worthy of further study. Otherwise, we cannot reject the null claim.

Organ donation consultants

One consultant tried to attract patients by noting that the average complication rate for liver donor surgeries in the US is about 10%, but her clients have only had 3 complications in the 62 liver donor surgeries she has facilitated. She claims this is strong evidence that her work meaningfully contributes to reducing complications (and therefore she should be hired!).

Is this a reasonable claim to make?

Organ donation consultants

Is there sufficient evidence to suggest that her complication rate is lower than the overall US rate?

The hypothesis testing framework

Start with two hypotheses about the population: the null hypothesis and the alternative hypothesis.
Choose a (representative) sample, collect data, and analyze the data.
Figure out how likely it is to see data like what we observed, IF the null hypothesis were in fact true.
If our data would have been extremely unlikely if the null claim were true, then we reject it and deem the alternative claim worthy of further study. Otherwise, we cannot reject the null claim.

Two competing hypotheses

The null hypothesis (often denoted $H_0$) states that “nothing unusual is happening” or “there is no relationship,” etc.

On the other hand, the alternative hypothesis (often denoted $H_1$ or $H_A$) states the opposite: that there is some sort of relationship.

In statistical hypothesis testing we always first assume that the null hypothesis is true and then evaluate the weight of proof we have against this claim.

1. Defining the hypotheses

The null and alternative hypotheses are defined for parameters.

What will our null and alternative hypotheses be for this example?

$H_0$: the true proportion of complications among her patients is equal to the US population rate
$H_1$: the true proportion of complications among her patients is less than the US population rate

Expressed in symbols:

$H_0: p = 0.10$
$H_1: p < 0.10$

where $p$ is the true proportion of transplants with complications among her patients.

2. Collecting and summarizing data

With these two hypotheses, we now take our sample and summarize the data.

The choice of summary statistic calculated depends on the type of data. In our example, we use the sample proportion: $\widehat{p} = 3/62 \approx 0.048$:

3. Assessing the evidence observed

Next, we calculate the probability of getting data like ours, or more extreme, if $H_0$ were in fact actually true.

This is a conditional probability:

Given that $H_0$ is true (i.e., if $p$ were actually 0.10), what would be the probability of observing $\widehat{p} = 3/62$?”

This probability is known as the p-value.

3. Assessing the evidence observed

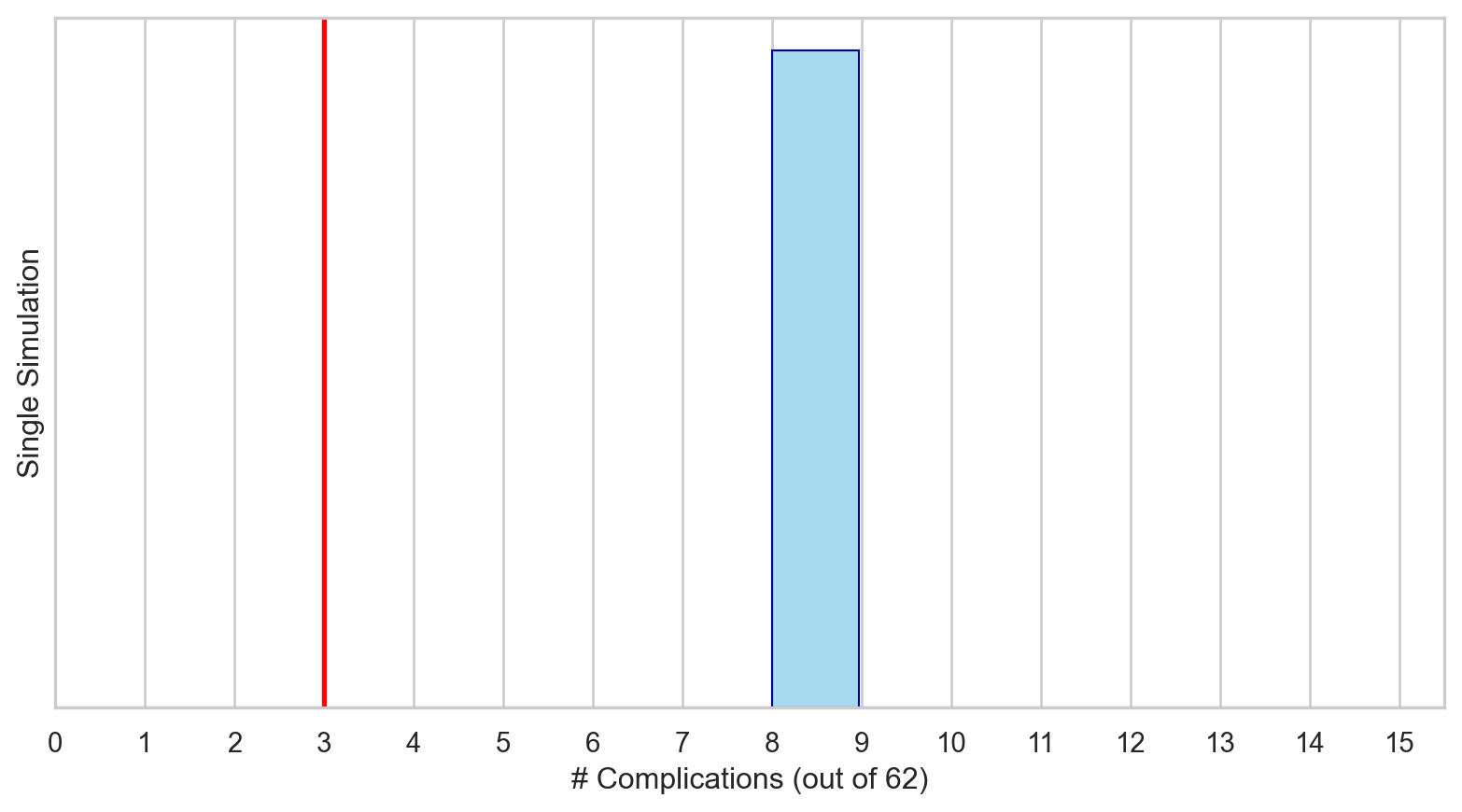
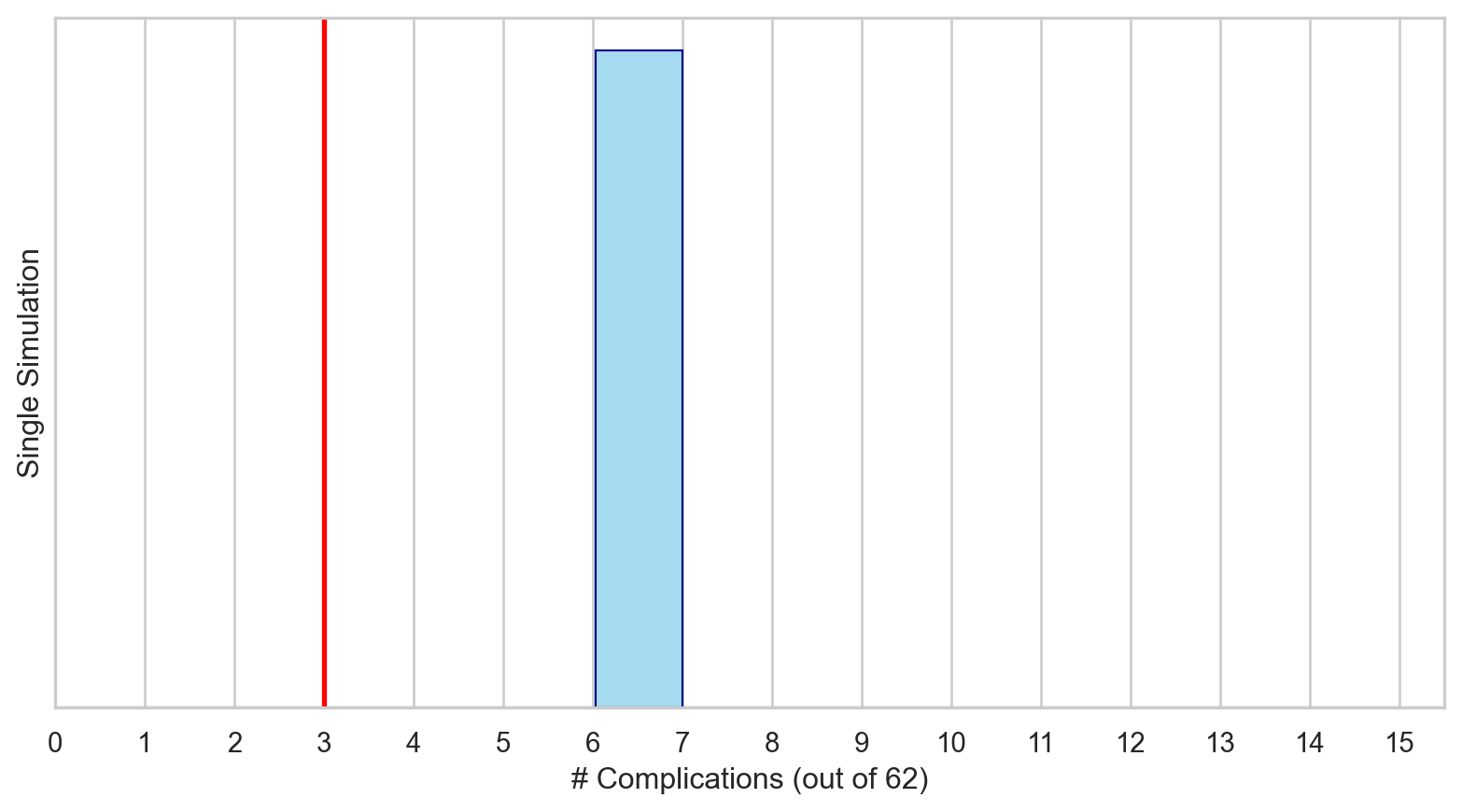
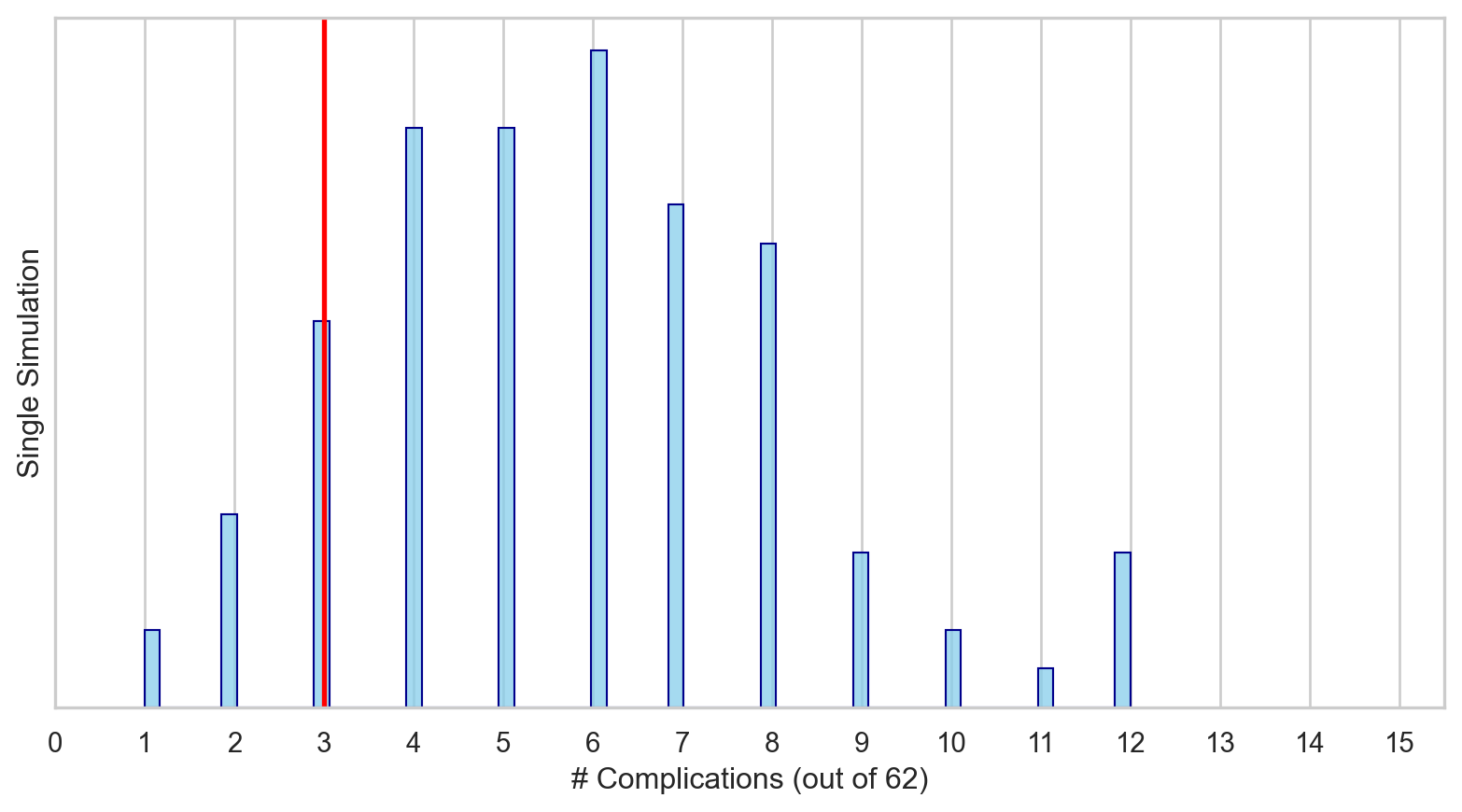
Let’s simulate a distribution for $\hat{p}$ such that the probability of complication for each patient is 0.10 for 62 patients.

This null distribution for $\hat{p}$ represents the distribution of the observed proportions we might expect, if the null hypothesis were true.

When sampling from the null distribution, what is the expected proportion of complications? What would the expected count be of patients experiencing complications?

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

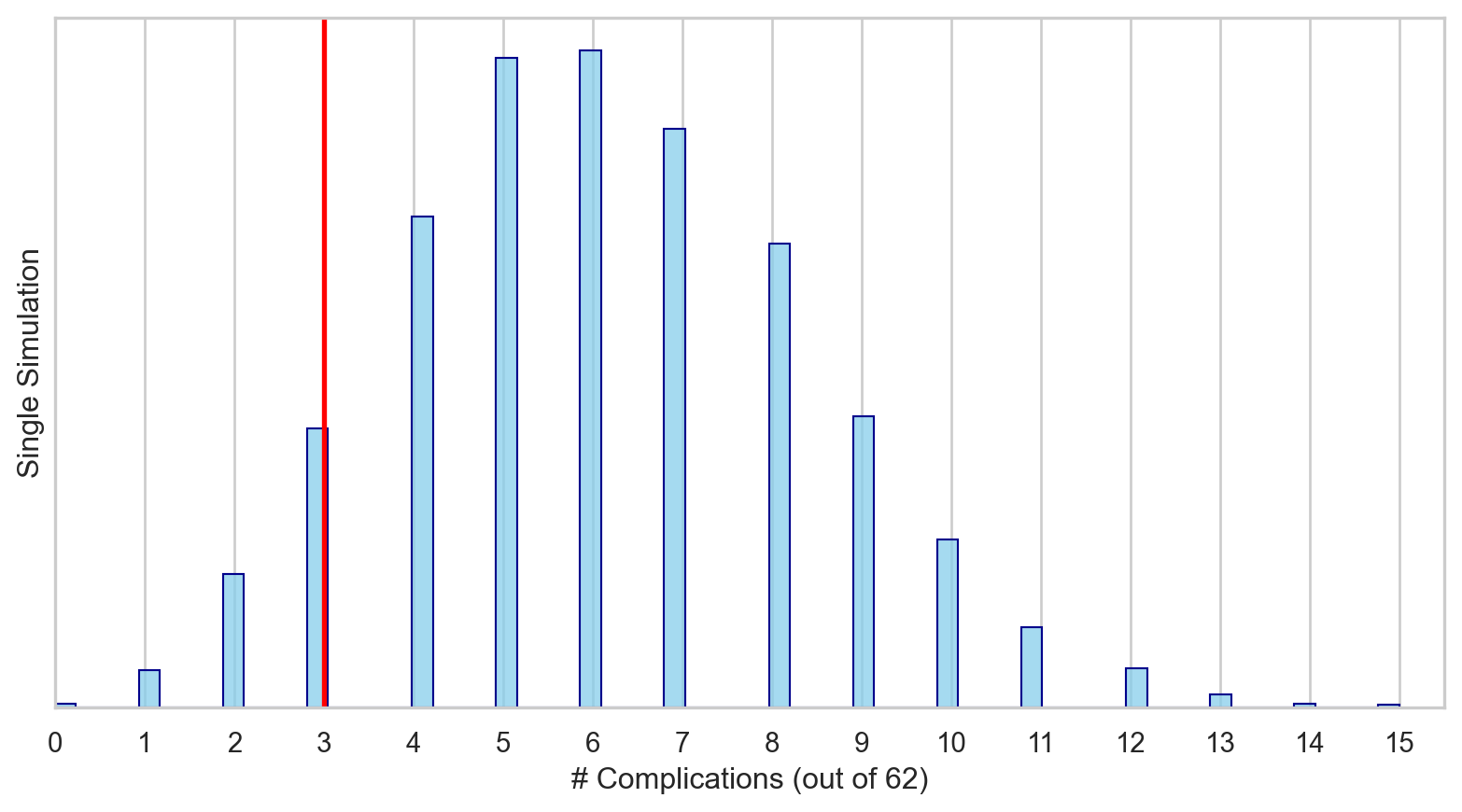
3. Assessing the evidence observed

Supposing that the true proportion of complications is 10%, if we were to take repeated samples of 62 liver transplants, about 11.5% of them would have 3 or fewer complications.

That is, p = 0.115.

4. Making a conclusion

If it is very unlikely to observe our data (or more extreme) if $H_0$ were actually true, then that might give us enough evidence to suggest that it is actually false (and that $H_1$ is true).

What is “small enough”?

We often consider a numeric cutpoint (the significance level) defined prior to conducting the analysis.
Many analyses use $\alpha = 0.05$. This means that if $H_0$ were in fact true, we would expect to make the wrong decision only 5% of the time.

If the p-value is less than $\alpha$, we say the results are statistically significant. In such a case, we would make the decision to reject the null hypothesis.

What do we conclude when $p \ge \alpha$?

If the p-value is $\alpha$ or greater, we say the results are not statistically significant and we fail to reject the null hypothesis.

Importantly, we never “accept” the null hypothesis – we performed the analysis assuming that $H_0$ was true to begin with and assessed the probability of seeing our observed data or more extreme under this assumption.

4. Making a conclusion

There is insufficient evidence at $\alpha = 0.05$ to suggest that the consultant’s complication rate is less than the US average.

Vacation rentals in Tucson, AZ

Your friend claims that the mean price per guest per night for Airbnbs in Tucson, AZ is $100. What do you make of this statement?

1. Defining the hypotheses

Remember, the null and alternative hypotheses are defined for parameters, not statistics

What will our null and alternative hypotheses be for this example?

$H_0$: the true mean price per guest is $100 per night
$H_1$: the true mean price per guest is NOT $100 per night

Expressed in symbols:

$H_0: \mu = 100$
$H_1: \mu \neq 100$

where $\mu$ is the true population mean price per guest per night among Airbnb listings in Tucson.

2. Collecting and summarizing data

With these two hypotheses, we now take our sample and summarize the data. We have a representative of 50 Airbnb listings in the file tucson.csv.

The choice of summary statistic calculated depends on the type of data. In our example, we use the sample proportion, $\bar{x} = 116.24$.

tucson = pd.read_csv('data/tucson.csv')

mean_price = tucson['ppg'].mean()
print(f"Sample mean price: {mean_price:.2f}")

Sample mean price: 116.24

3. Assessing the evidence observed

We know that not every representative sample of 50 Airbnb listings in Tucson will have exactly a sample mean of exactly $116.24.

How might we deal with this variability in the sampling distribution of the mean using only the data that we have from our original sample?

We can take bootstrap samples, formed by sampling with replacement from our original dataset, of the same sample size as our original dataset.

3. Assessing the evidence observed

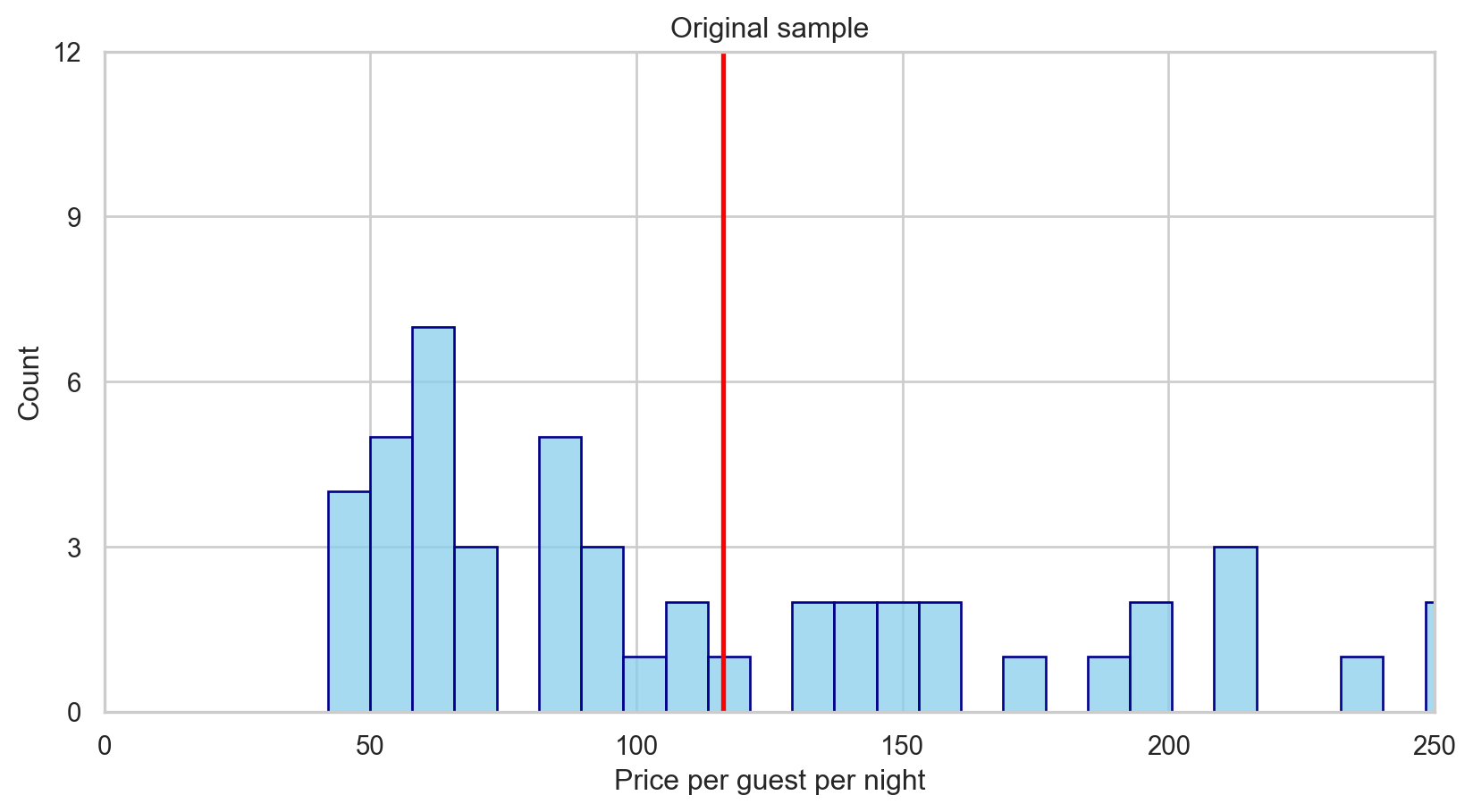
Mean price per guest per night: 116.24

3. Assessing the evidence observed

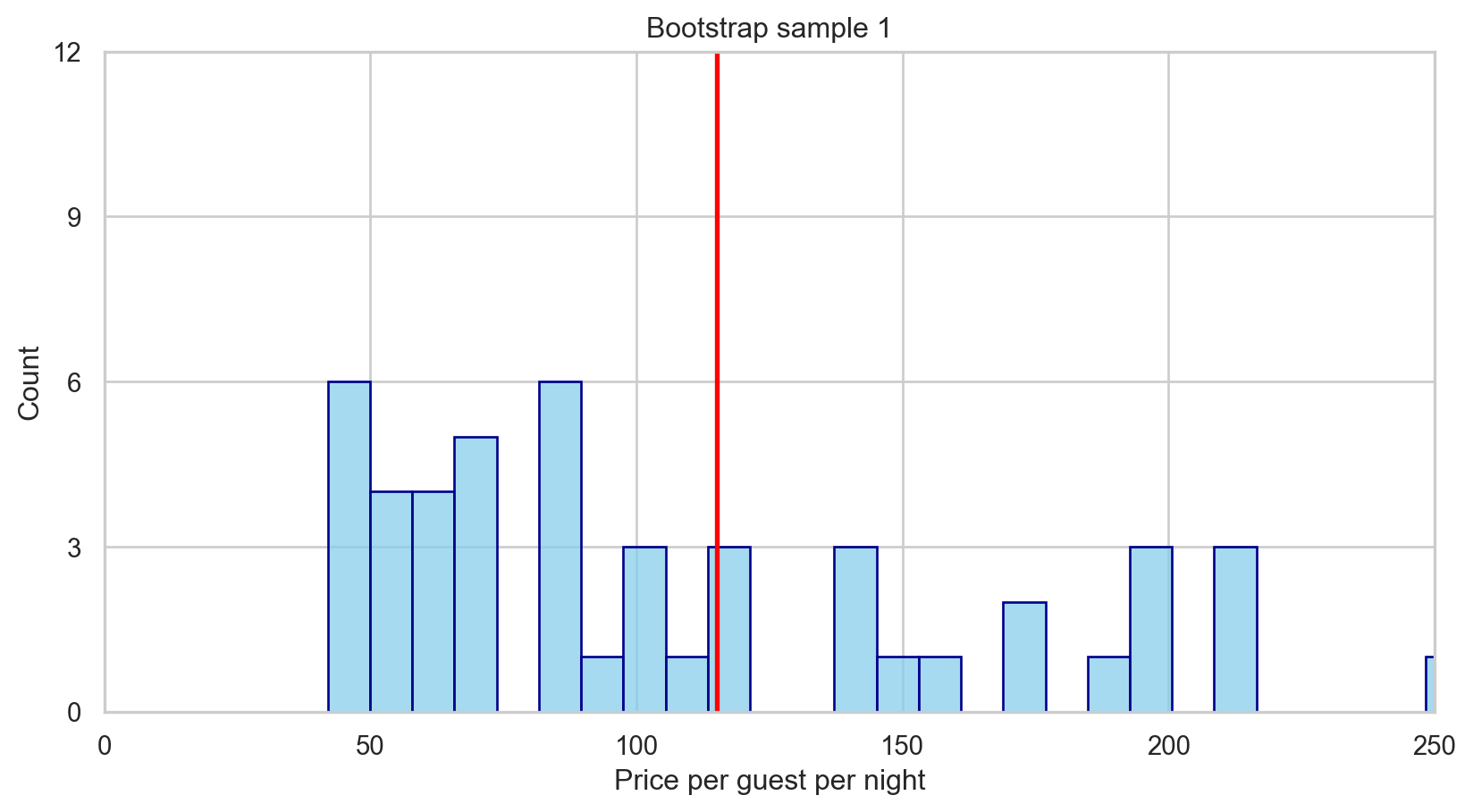
Mean price per guest per night (Bootstrap 1): 115.20

3. Assessing the evidence observed

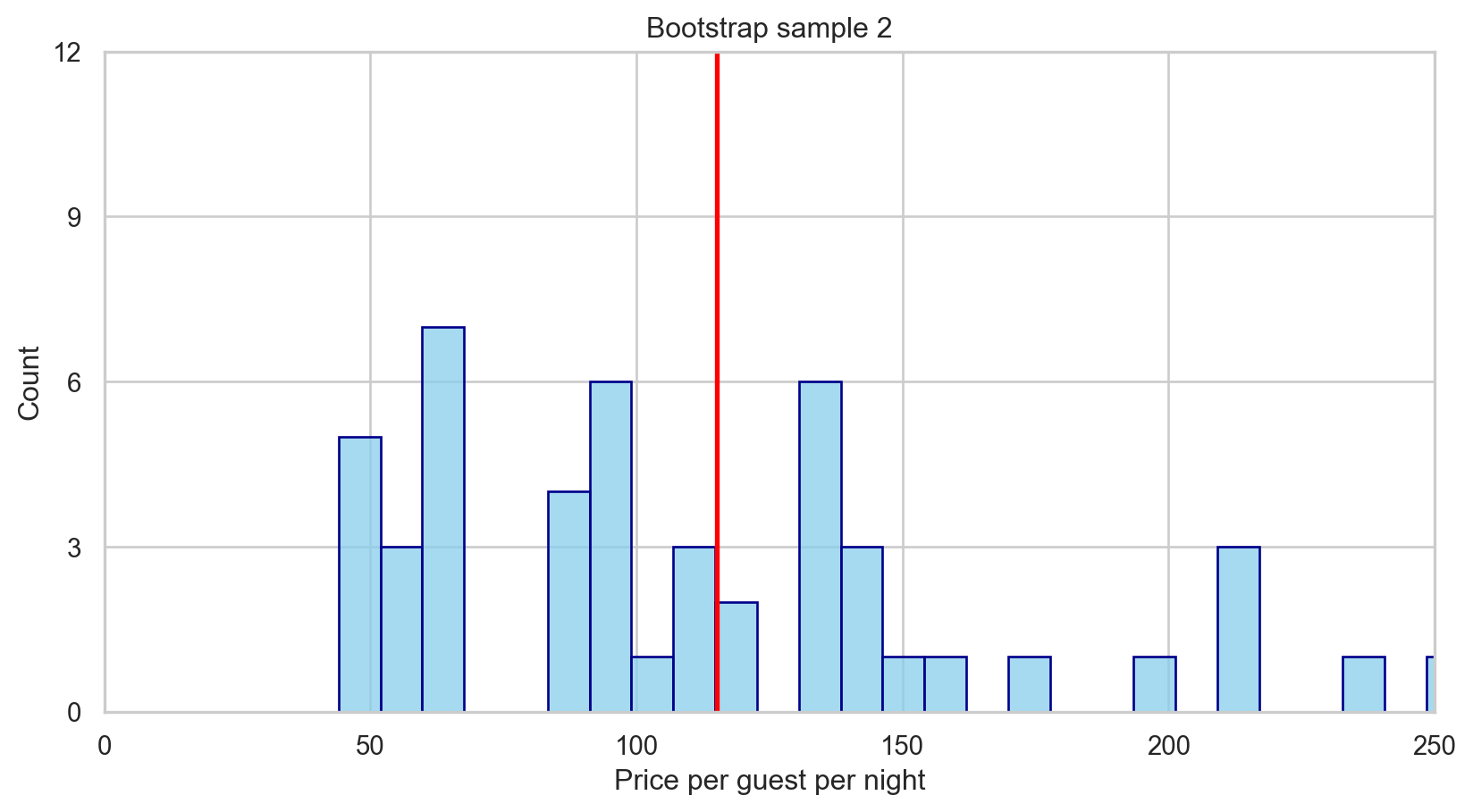
Mean price per guest per night (Bootstrap 2): 115.08

3. Assessing the evidence observed

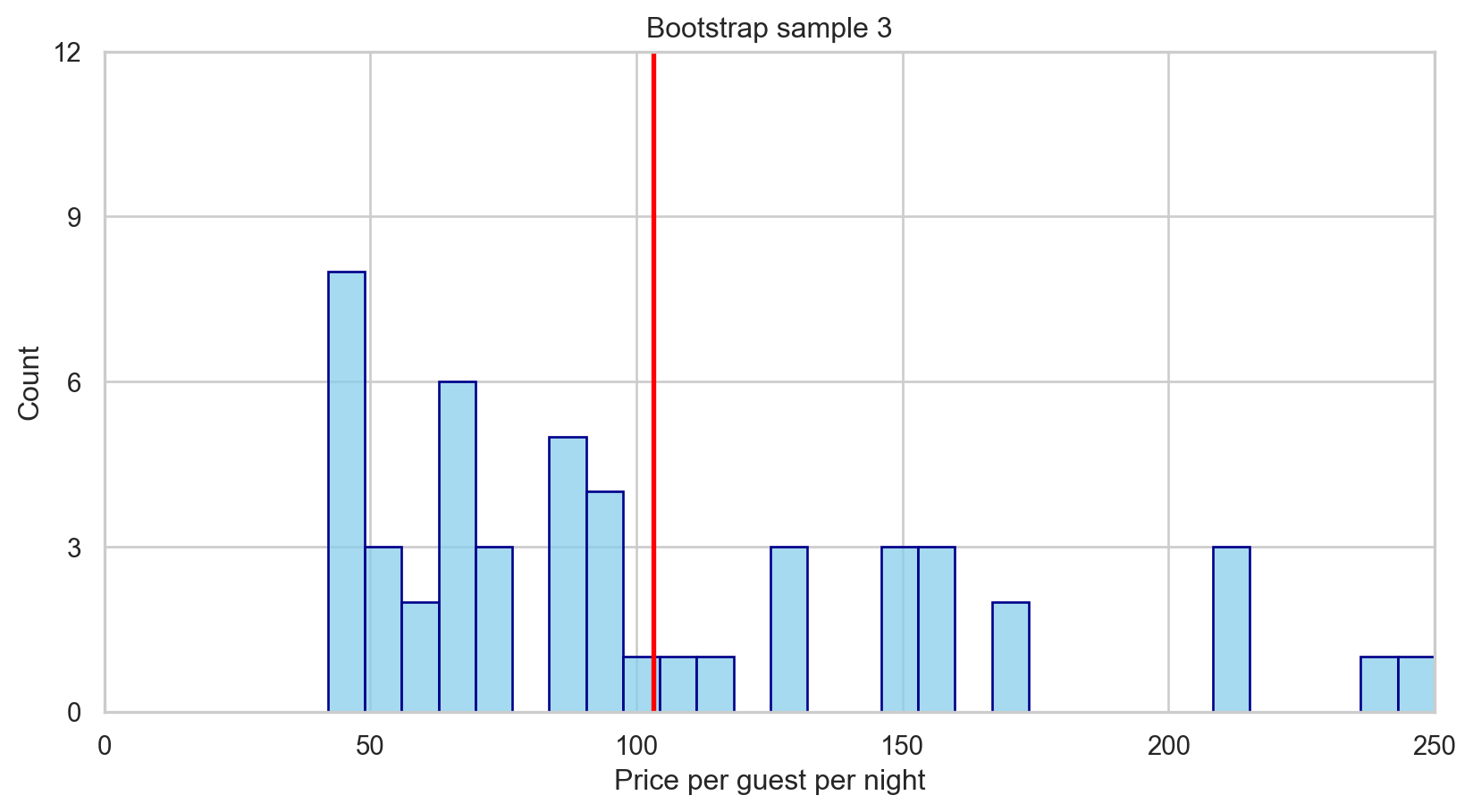
Mean price per guest per night (Bootstrap 3): 103.20

3. Assessing the evidence observed

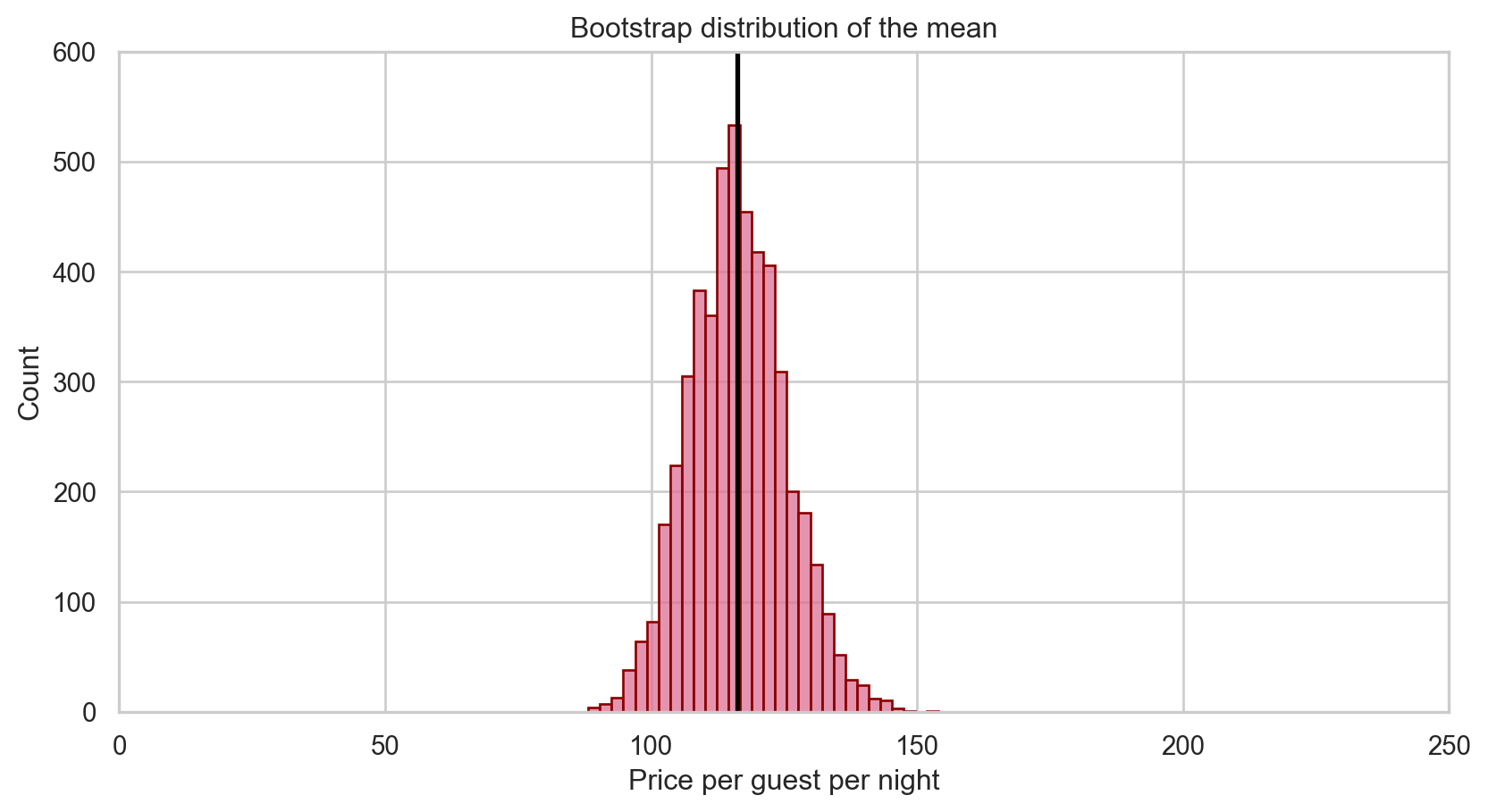
Mean of bootstrap means: 116.24

Shifting the distribution

We’ve captured the variability in the sample mean among samples of size 50 from Tucson area Airbnbs, but remember that in the hypothesis testing paradigm, we must assess our observed evidence under the assumption that $H_0$ is true.

mean_price = bootstrap_means_df['boot_means'].mean()
print(f"Sample mean price: {mean_price:.2f}")

Sample mean price: 116.24

Where should the bootstrap distribution of means be centered under $H_0$?

Shifting the distribution

Mean of bootstrap means: 116.24

Shifting the distribution

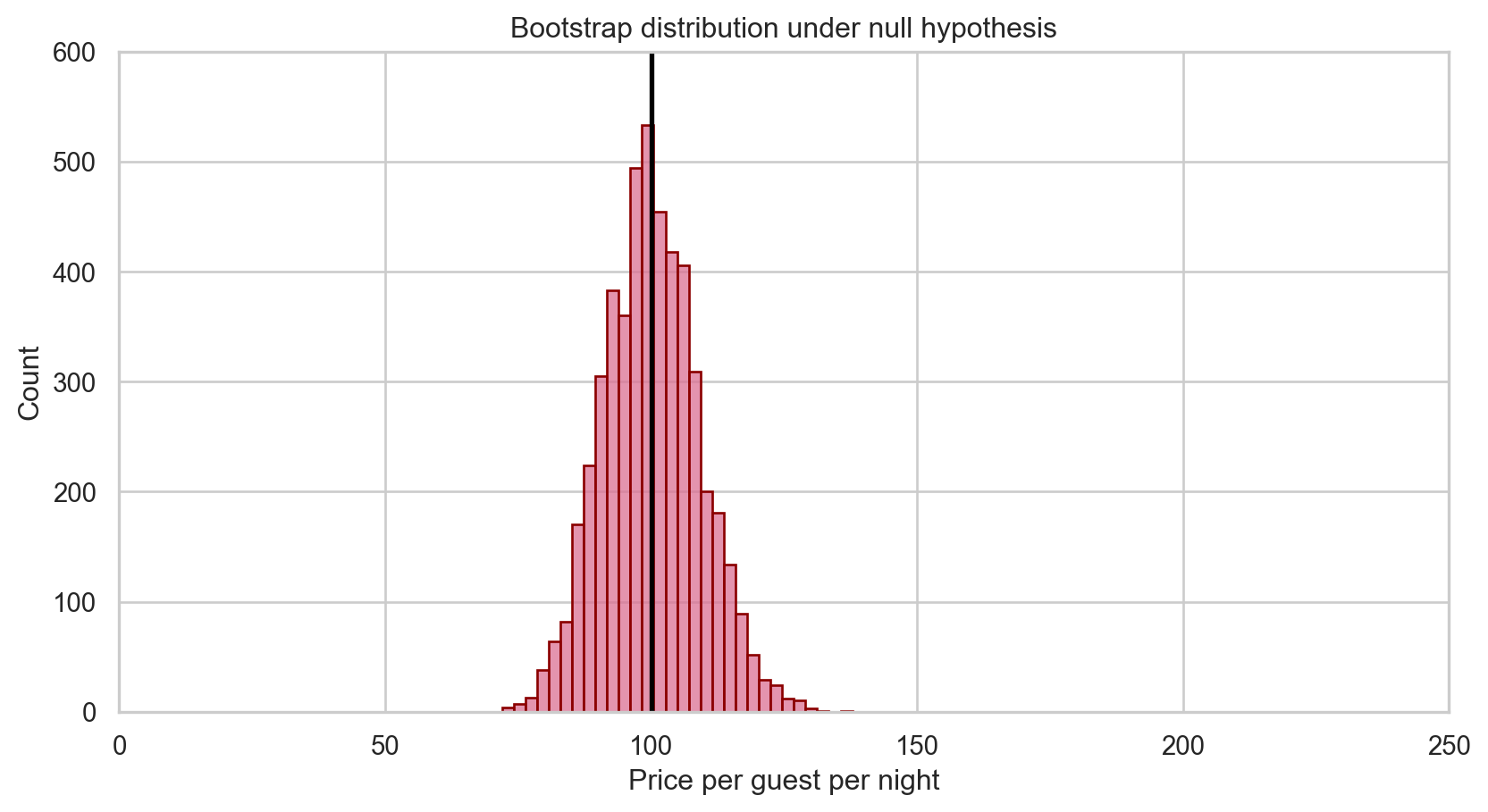
3. Assessing the evidence observed

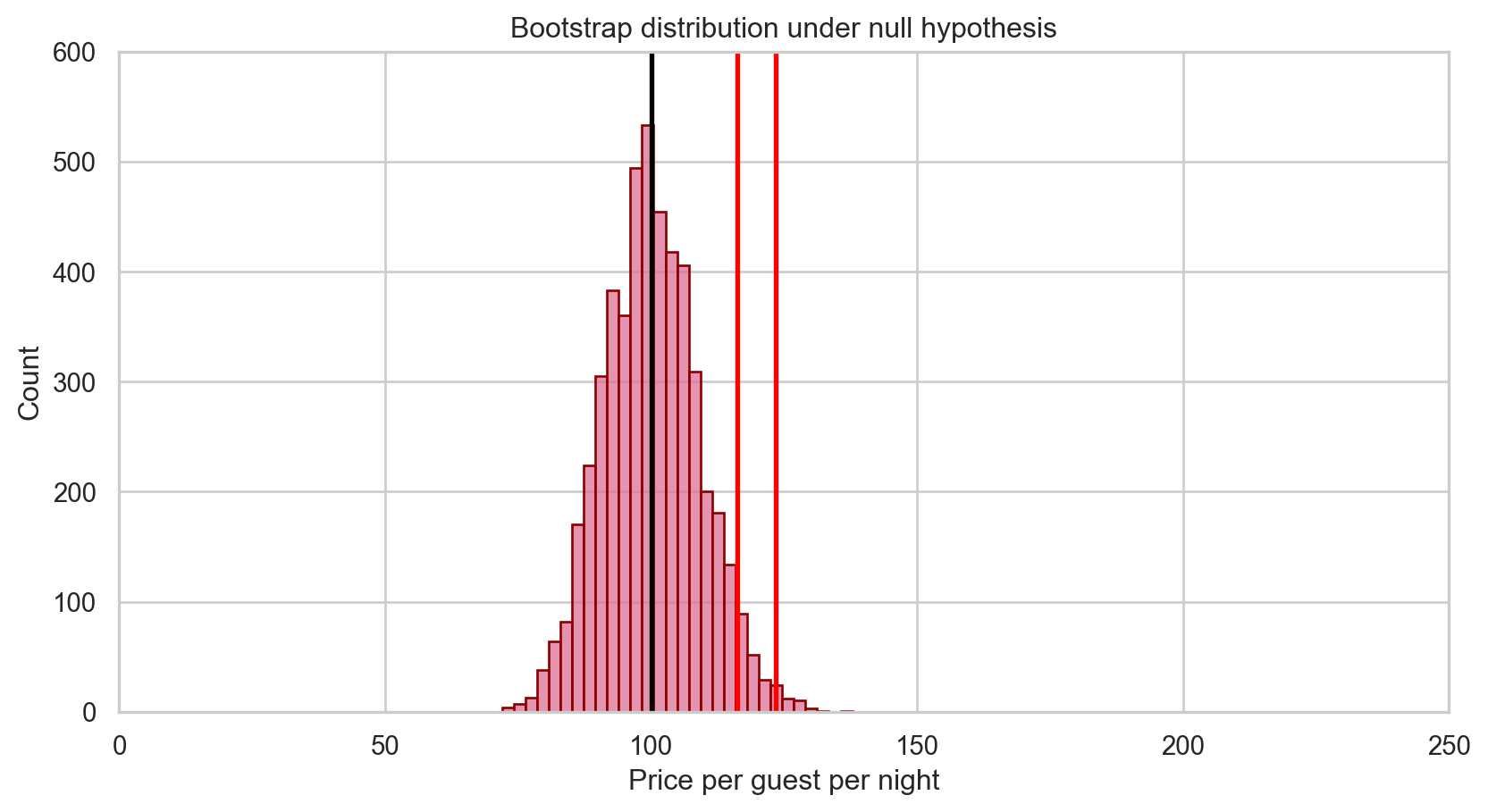
3. Assessing the evidence observed

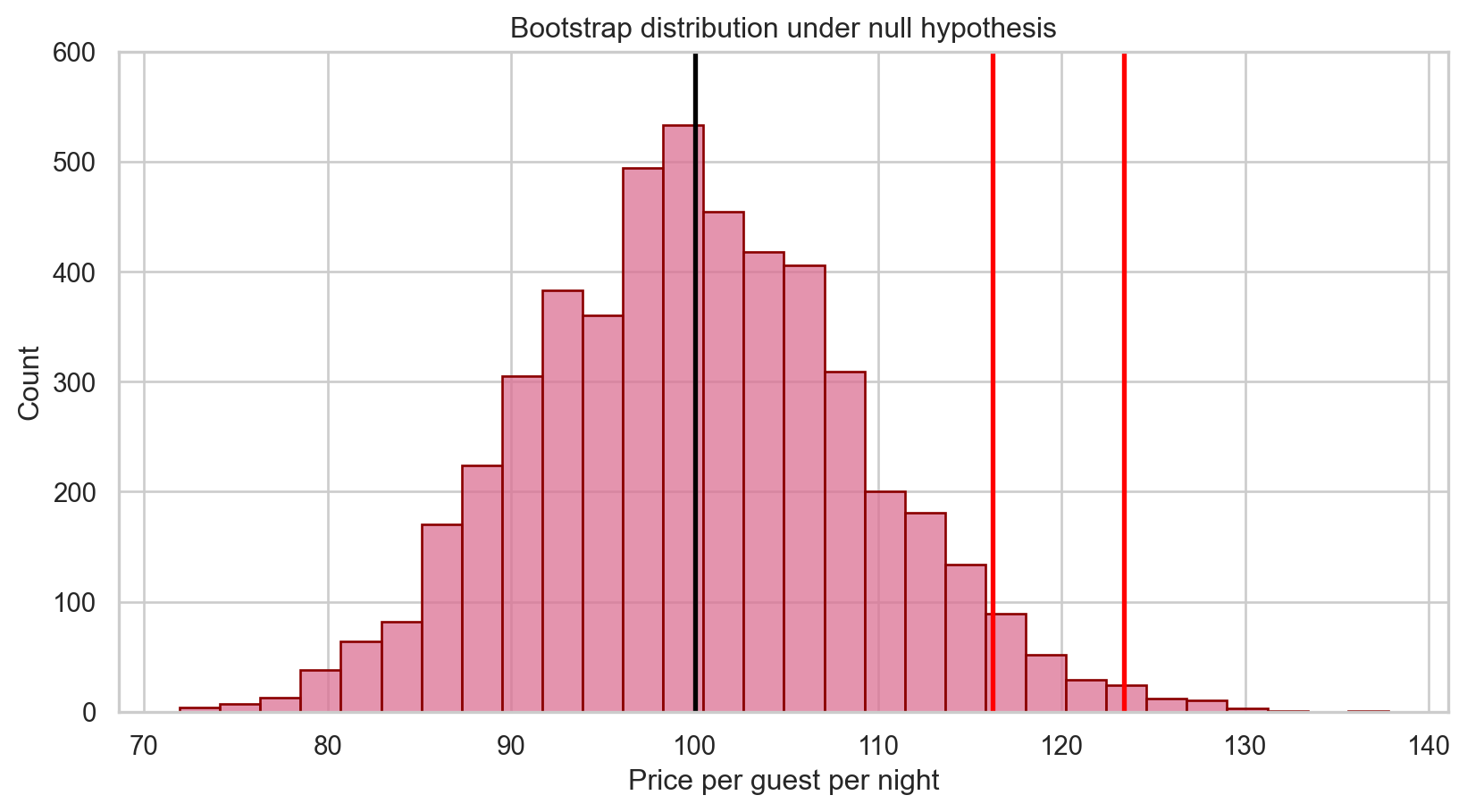
3. Assessing the evidence observed

Supposing that the true mean price per guest were $100 a night, about 0.16% of bootstrap sample means were as extreme or even more so than our originally observed sample mean price per guest of $116.24.

That is, p = 0.0016.

4. Making a conclusion

If it is very unlikely to observe our data (or more extreme) if $H_0$ were actually true, then that might give us enough evidence to suggest that it is actually false (and that $H_1$ is true).

There is sufficient evidence at $\alpha = 0.05$ to suggest that the mean price per guest per night of Airbnb rentals in Tucson is not $100.

Ok, so what isn’t a p-value?

“A p-value of 0.05 means the null hypothesis has a probability of only 5% of being true”

“A p-value of 0.05 means there is a 95% chance or greater that the null hypothesis is incorrect”

p-values do not provide information on the probability that the null hypothesis is true given our observed data.

What can go wrong?

Remember, a p-value is calculated assuming that $H_0$ is true. It cannot be used to tell us how likely that assumption is correct. When we fail to reject the null hypothesis, we are stating that there is insufficient evidence to assert that it is false. This could be because…

… $H_0$ actually is true!
… $H_0$ is false, but we got unlucky and happened to get a sample that didn’t give us enough reason to say that $H_0$ was false.

Even more bad news, hypothesis testing does NOT give us the tools to determine which one of the two scenarios occurred.

What can go wrong?

Suppose we test a certain null hypothesis, which can be either true or false (we never know for sure!). We make one of two decisions given our data: either reject or fail to reject $H_0$.

We have the following four scenarios:

Decision	$H_0$ is true	$H_0$ is false
Fail to reject $H_0$	Correct decision	Type II Error
Reject $H_0$	Type I Error	Correct decision

$\alpha$ is the probability of making a Type I error.
$\beta$ is the probability of making a Type II error.
The power of a test is 1 - $\beta$: the probability that, if the null hypothesis is actually false, we correctly reject it.

`ae-09`

Work through the Tucson Airbnb prices data in an exercise on Quantifying uncertainty

Decision	\(H_0\) is true	\(H_0\) is false
Fail to reject \(H_0\)	Correct decision	Type II Error
Reject \(H_0\)	Type I Error	Correct decision

Hypothesis testing

Setup

Hypothesis testing

How can we answer questions using statistics?

The hypothesis testing framework

The hypothesis testing framework

Organ donation consultants

Organ donation consultants

Organ donation consultants

Organ donation consultants

The hypothesis testing framework

Two competing hypotheses

1. Defining the hypotheses

2. Collecting and summarizing data

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

4. Making a conclusion

What do we conclude when \(p \ge \alpha\)?

4. Making a conclusion

Vacation rentals in Tucson, AZ

1. Defining the hypotheses

2. Collecting and summarizing data

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

Shifting the distribution

Shifting the distribution

Shifting the distribution

3. Assessing the evidence observed

3. Assessing the evidence observed

3. Assessing the evidence observed

4. Making a conclusion

Ok, so what isn’t a p-value?

What can go wrong?

What can go wrong?

ae-09

`ae-09`