Exploratory data analysis

Lecture 4

Dr. Greg Chism

University of Arizona
INFO 511 - Fall 2024

Setup

# Import all required libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stats
from scipy.stats import skewnorm
from scipy.stats import kurtosis, norm
from scipy.stats import gamma
import missingno as msno
import random
import statsmodels.api as sm

# Load in UK Smoking Data
births14 = pd.read_csv("data/births14.csv")

# Set seed
random.seed(123)

Exploratory Data Analysis

What is exploratory data analysis?

Exploratory Data Analysis is a statistical approach to analyzing datasets to summarize their main characteristics, often using visual methods.

Examining data

births14.head()
fage mage mature weeks premie visits gained weight lowbirthweight sex habit marital whitemom
0 34.0 34 younger mom 37 full term 14.0 28.0 6.96 not low male nonsmoker married white
1 36.0 31 younger mom 41 full term 12.0 41.0 8.86 not low female nonsmoker married white
2 37.0 36 mature mom 37 full term 10.0 28.0 7.51 not low female nonsmoker married not white
3 NaN 16 younger mom 38 full term NaN 29.0 6.19 not low male nonsmoker not married white
4 32.0 31 younger mom 36 premie 12.0 48.0 6.75 not low female nonsmoker married white 
births14.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 13 columns):
 #   Column          Non-Null Count  Dtype  
---  ------          --------------  -----  
 0   fage            886 non-null    float64
 1   mage            1000 non-null   int64  
 2   mature          1000 non-null   object 
 3   weeks           1000 non-null   int64  
 4   premie          1000 non-null   object 
 5   visits          944 non-null    float64
 6   gained          958 non-null    float64
 7   weight          1000 non-null   float64
 8   lowbirthweight  1000 non-null   object 
 9   sex             1000 non-null   object 
 10  habit           981 non-null    object 
 11  marital         1000 non-null   object 
 12  whitemom        1000 non-null   object 
dtypes: float64(4), int64(2), object(7)
memory usage: 101.7+ KB
births14.describe()
fage mage weeks visits gained weight
count 886.000000 1000.000000 1000.000000 944.000000 958.000000 1000.000000
mean 31.133183 28.449000 38.666000 11.351695 30.425887 7.198160
std 7.058135 5.759737 2.564961 4.108192 15.242527 1.306775
min 15.000000 14.000000 21.000000 0.000000 0.000000 0.750000
25% 26.000000 24.000000 38.000000 9.000000 20.000000 6.545000
50% 31.000000 28.000000 39.000000 12.000000 30.000000 7.310000
75% 35.000000 33.000000 40.000000 14.000000 38.000000 8.000000
max 85.000000 47.000000 46.000000 30.000000 98.000000 10.620000

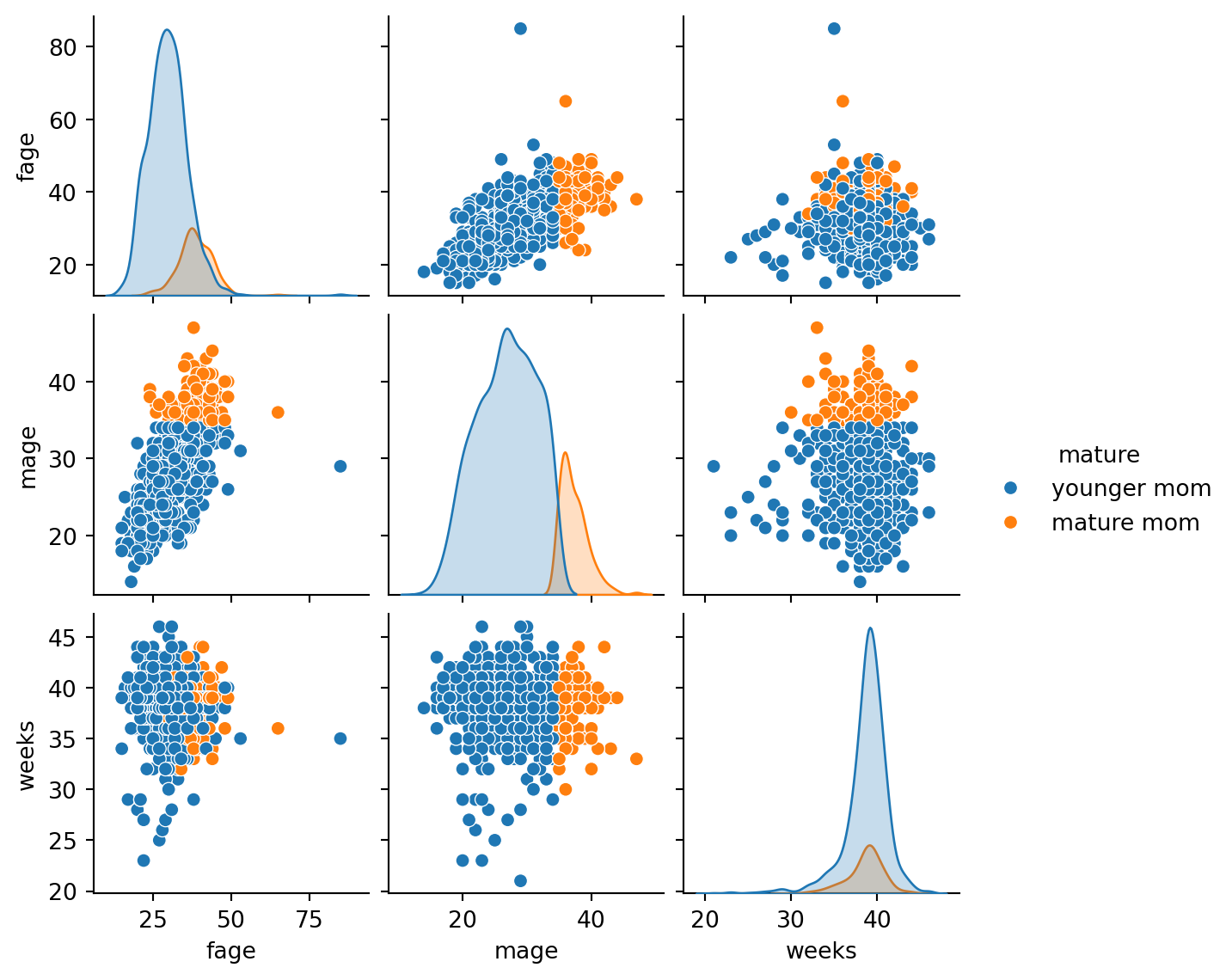
Visualizing data relationships

sns.pairplot(births14[['fage', 'mage', 'weeks', 'mature']], hue='mature', height=2)
plt.show()

Group descriptive statistics

# Example with the premie column
births14.groupby('premie').describe()
fage mage ... gained weight
count mean std min 25% 50% 75% max count mean ... 75% max count mean std min 25% 50% 75% max
premie
full term 775.0 30.967742 6.681591 15.0 26.0 31.0 35.0 49.0 876.0 28.329909 ... 38.0 98.0 876.0 7.434178 1.021699 3.93 6.77 7.44 8.0825 10.62
premie 111.0 32.288288 9.226826 15.0 27.0 32.0 36.0 85.0 124.0 29.290323 ... 41.0 85.0 124.0 5.530806 1.801182 0.75 4.50 5.75 6.5725 9.25

2 rows × 48 columns

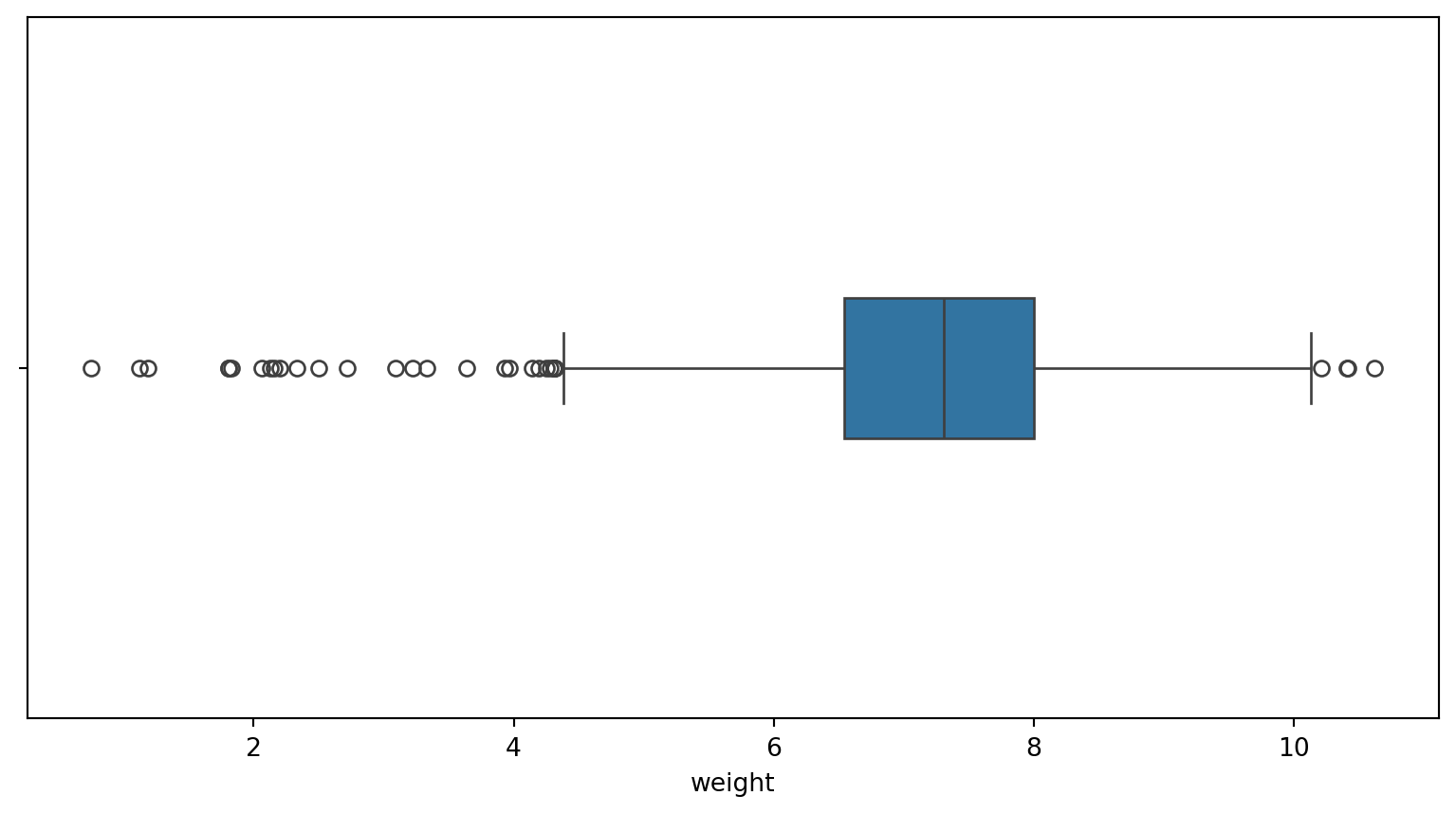
Outliers

Outliers are data points that are significantly different from others. Identifying and handling outliers is important in data analysis.

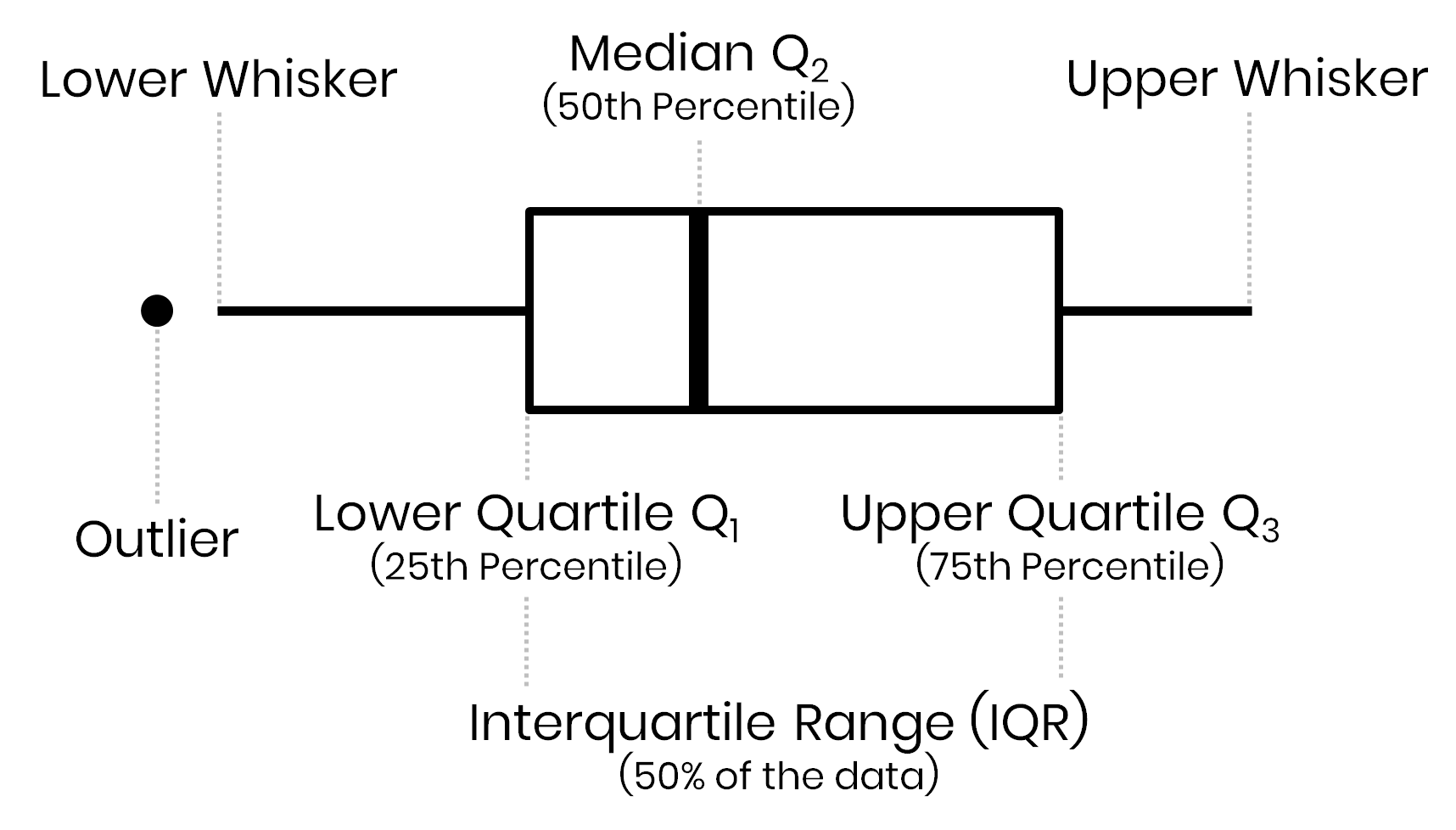
Outliers = 1.5 * Interquartile range

Assess outliers visually

sns.boxplot(data = births14, x = 'weight', width = 0.20)
plt.show()

Find outliers

fage: 7 outliers
mage: 1 outliers
weeks: 72 outliers
visits: 30 outliers
gained: 26 outliers
weight: 32 outliers
for column in births14.select_dtypes(include=np.number).columns:
    q25 = births14[column].quantile(0.25)
    q75 = births14[column].quantile(0.75)
    iqr = q75 - q25
    lower_bound = q25 - 1.5 * iqr
    upper_bound = q75 + 1.5 * iqr
    outliers = births14[(births14[column] < lower_bound) | (births14[column] > upper_bound)]
    print(f"{column}: {outliers.shape[0]} outliers")

  • q25: 1/4 quartile, 25th percentile; q75: 3/4 quartile, 75th percentile

  • IQR: interquartile range, \(IQR = q75-q25\)

  • lower; upper: lower, upper limit of \(1.5\times IQR\) used to calculate outliers

Remove outliers

# Select numerical columns
numerical_cols = births14.select_dtypes(include = ['number']).columns

for col in numerical_cols:
    # Find Q1, Q3, and interquartile range (IQR) for each column
    Q1 = births14[col].quantile(0.25)
    Q3 = births14[col].quantile(0.75)
    IQR = Q3 - Q1
    # Upper and lower bounds for each column
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    # Filter out the outliers from the DataFrame
    births14_clean = births14[(births14[col] >= lower_bound) & (births14[col] <= upper_bound)]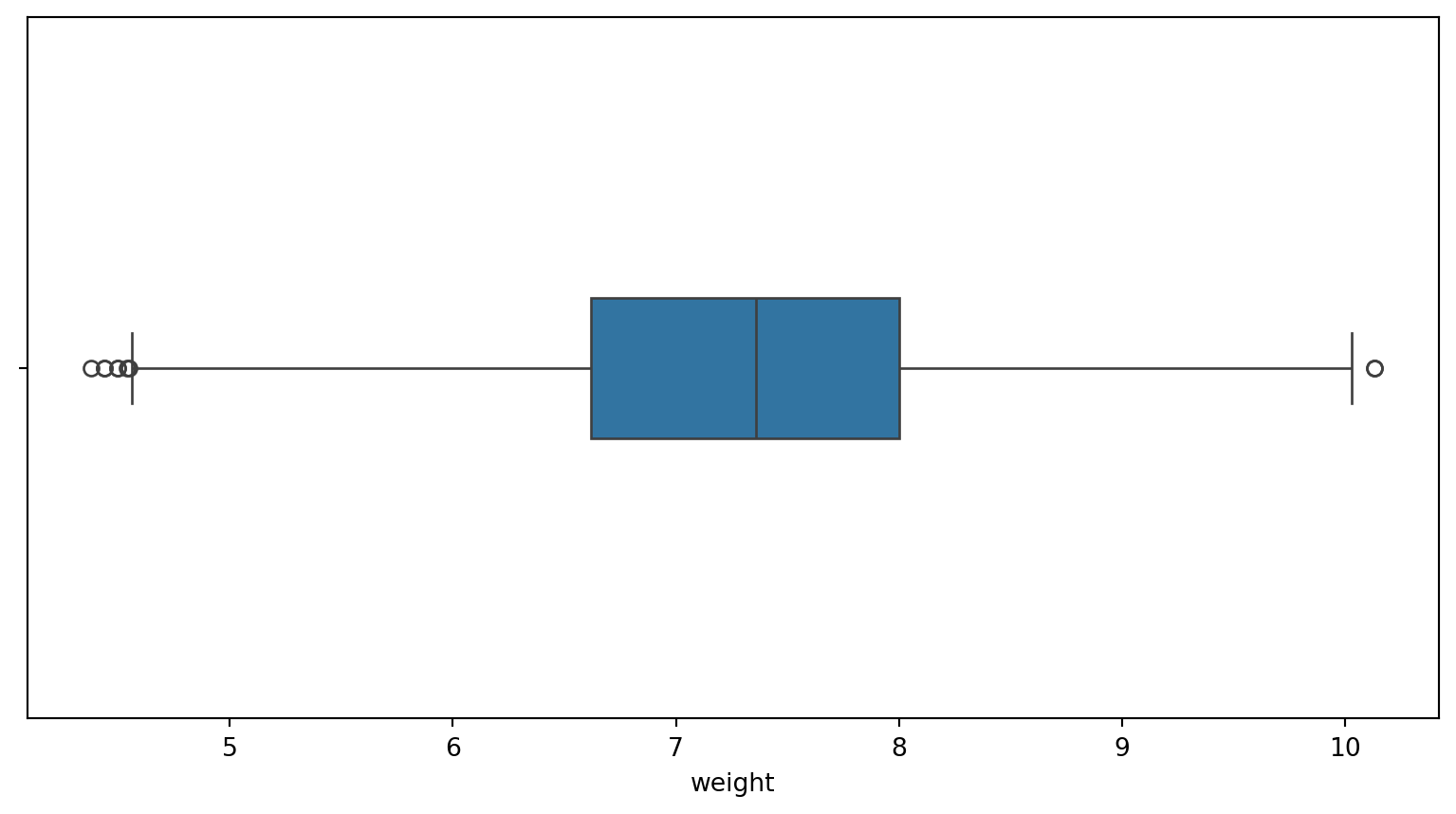

Why are there still outliers?

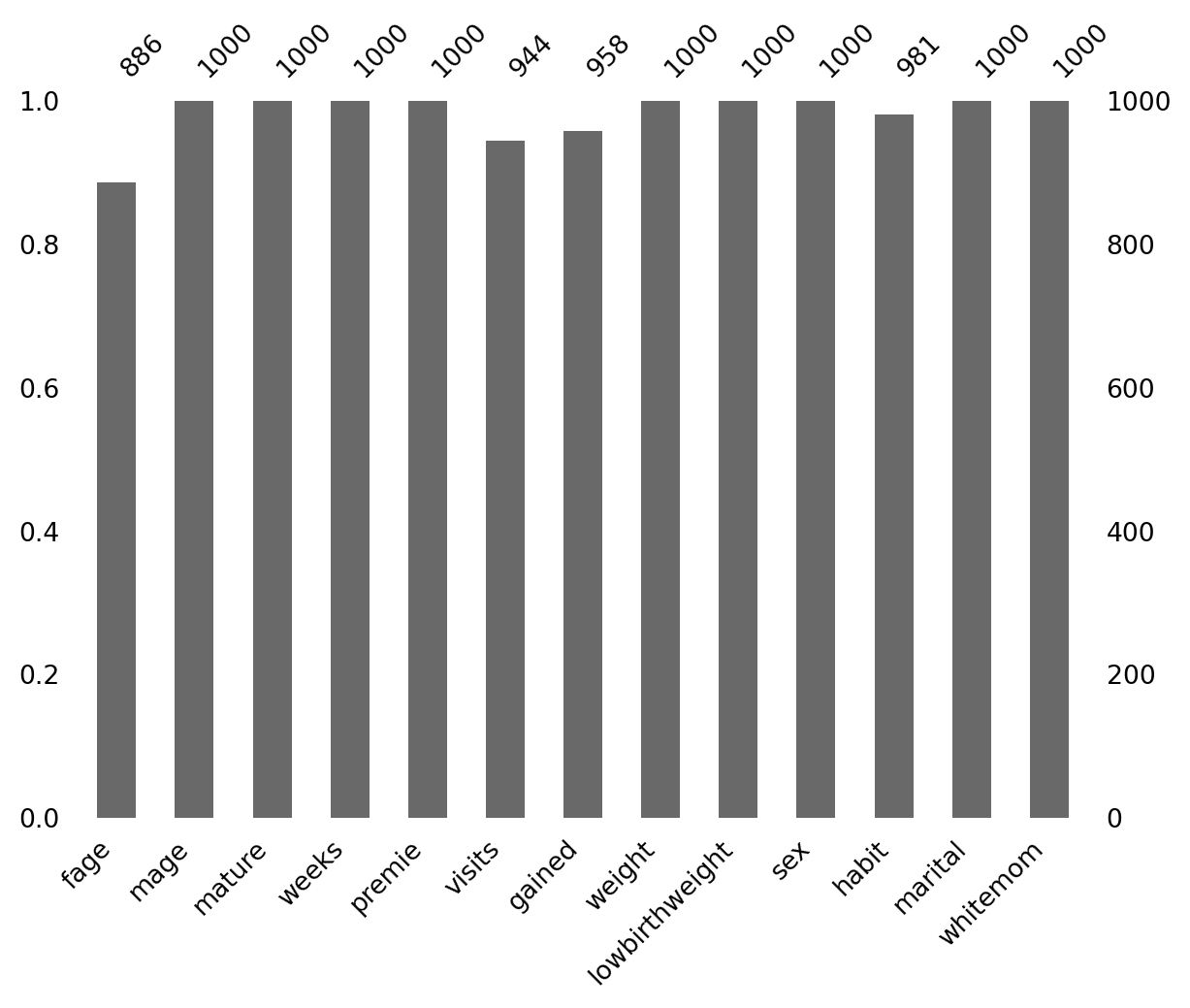
Missing values (NaN)

# Count missing values in each column
births14.isnull().sum()
fage              114
mage                0
mature              0
weeks               0
premie              0
visits             56
gained             42
weight              0
lowbirthweight      0
sex                 0
habit              19
marital             0
whitemom            0
dtype: int64

Visualizing (NaN)

We can use the missingno library to visualize missing data.

msno.bar(births14, figsize = (7, 5), fontsize = 10)
plt.show()

Describe categorical variables

births14.describe(exclude = [np.number])
mature premie lowbirthweight sex habit marital whitemom
count 1000 1000 1000 1000 981 1000 1000
unique 2 2 2 2 2 2 2
top younger mom full term not low male nonsmoker married white
freq 841 876 919 505 867 594 765 
mature: ['younger mom' 'mature mom']
premie: ['full term' 'premie']
lowbirthweight: ['not low' 'low']
sex: ['male' 'female']
habit: ['nonsmoker' 'smoker' nan]
marital: ['married' 'not married']
whitemom: ['white' 'not white']
for column in births14.select_dtypes(include=['object', 'category']).columns:
    print(f"{column}: {births14[column].unique()}")

Normality check

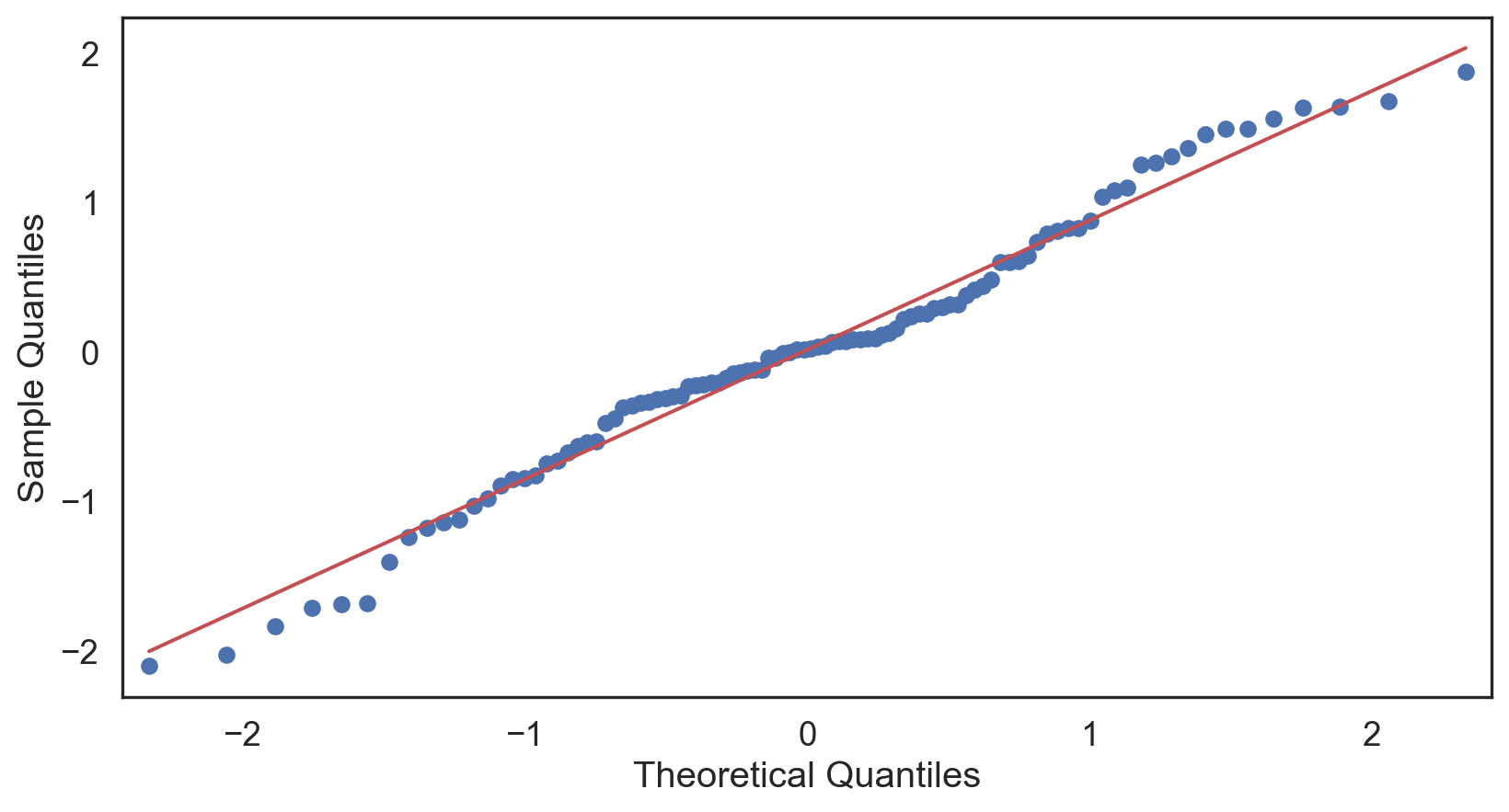
Checking if the data follows a normal distribution is a common step in EDA.

Normality check

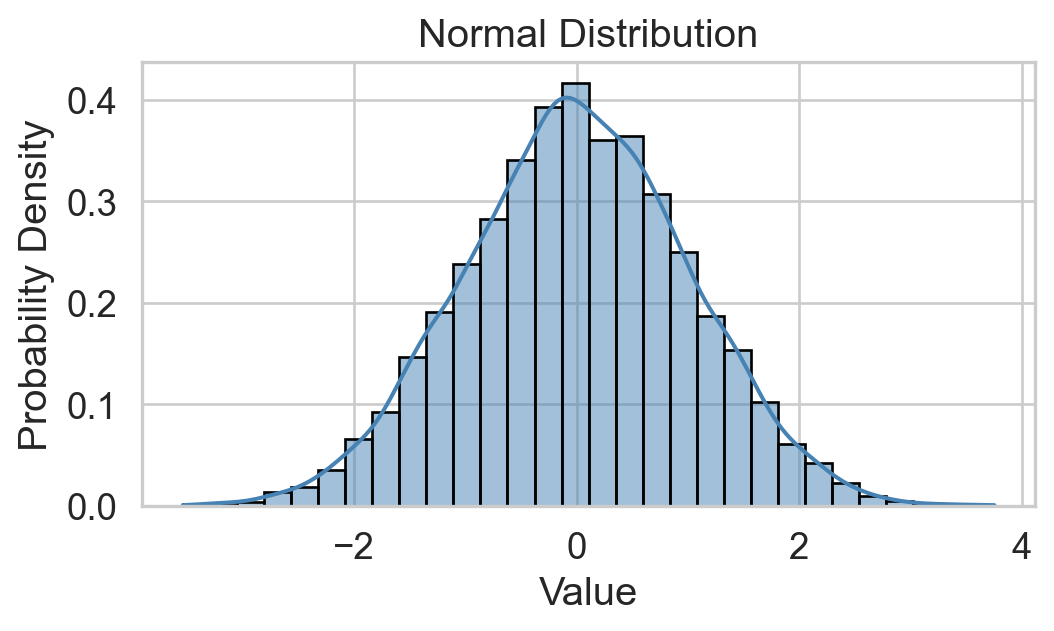
  • Histogram: bell-shaped curve

  • Skewness: Close to 0 for symmetry; Kurtosis: Close to 3 for normal “tailedness.”

  • Sample Size: Larger samples are less sensitive to non-normality.

  • Empirical Rule: 68-95-99.7% rule (1, 2, and 3 st dev. of the mean).

Skewness

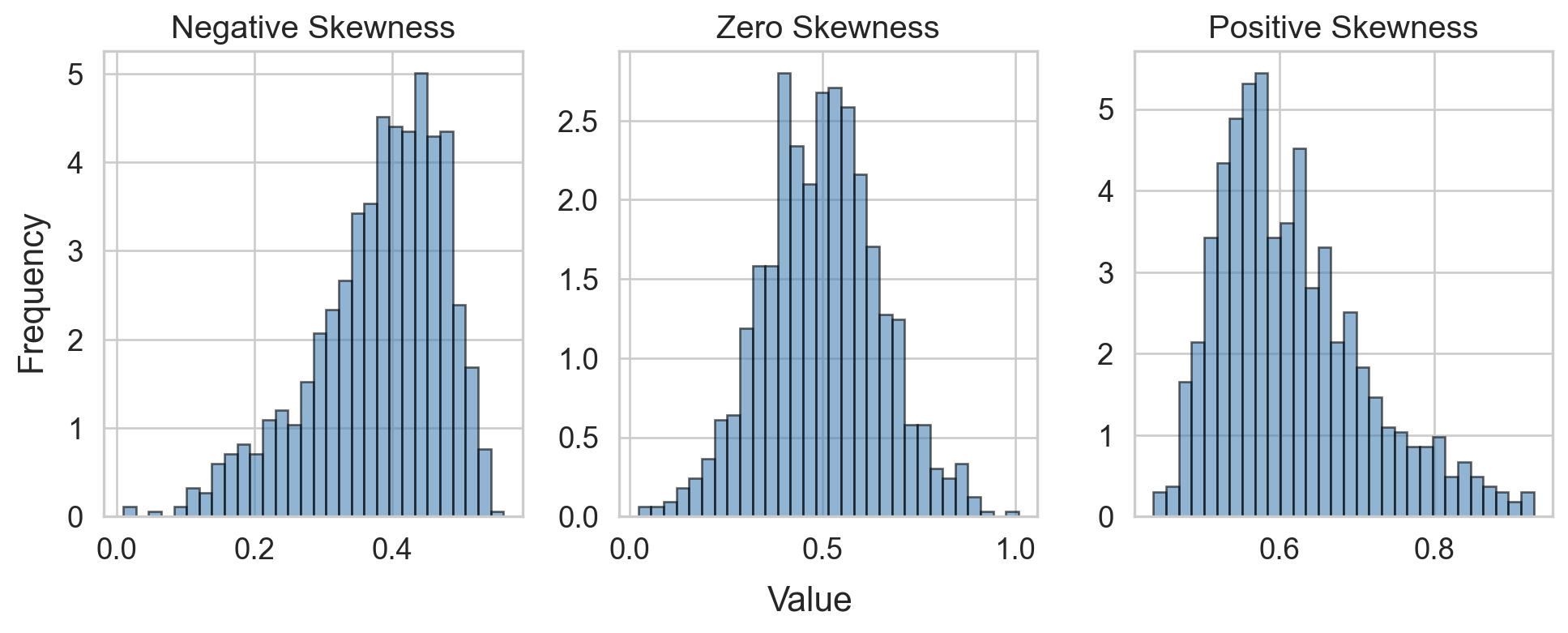
  • Several definitions
  • Sensitive to outliers
  • Designed for one peak (unimodal)

Kurtosis

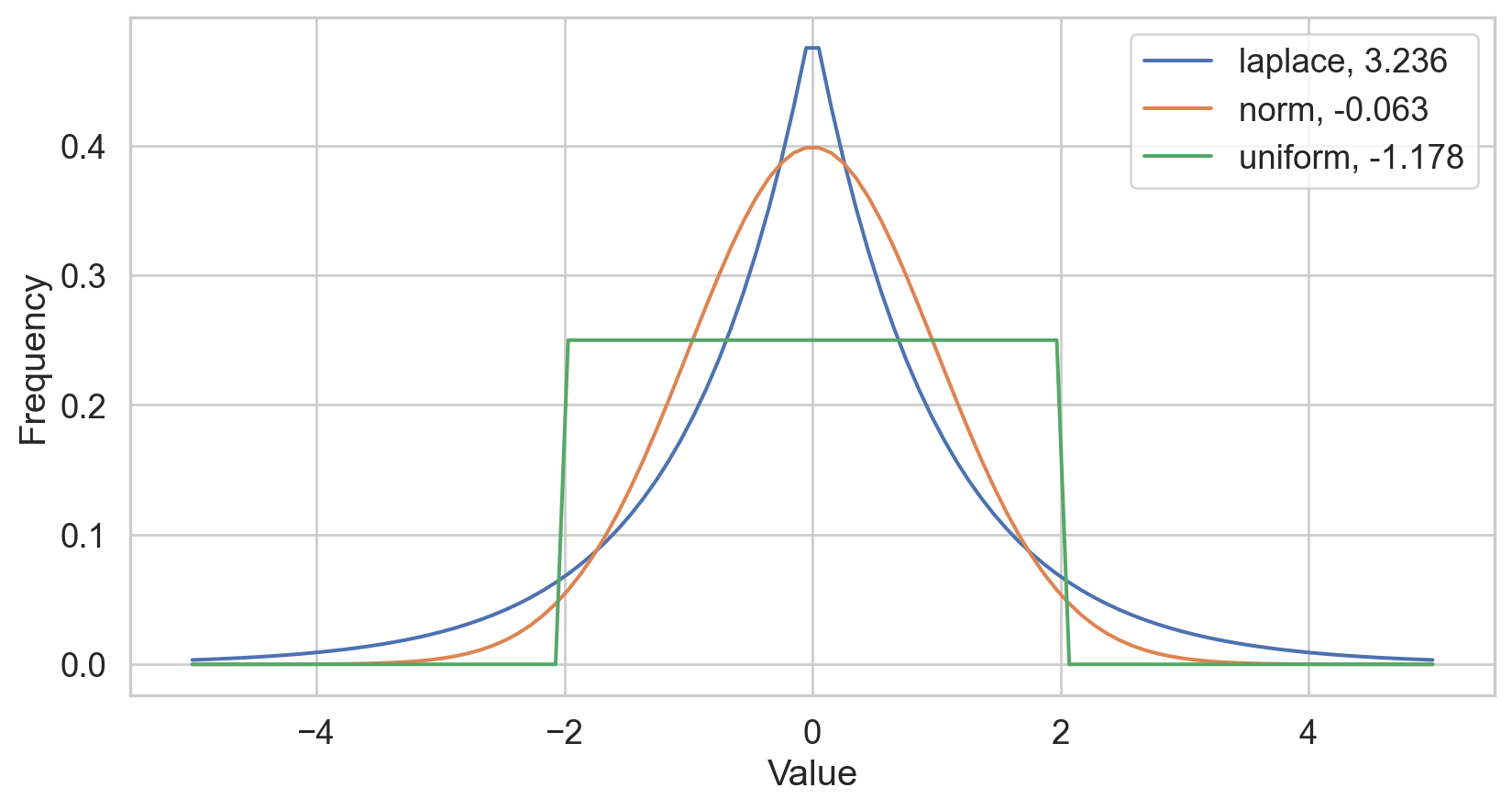
  • Sensitive to outliers
  • Designed for one peak (unimodal)

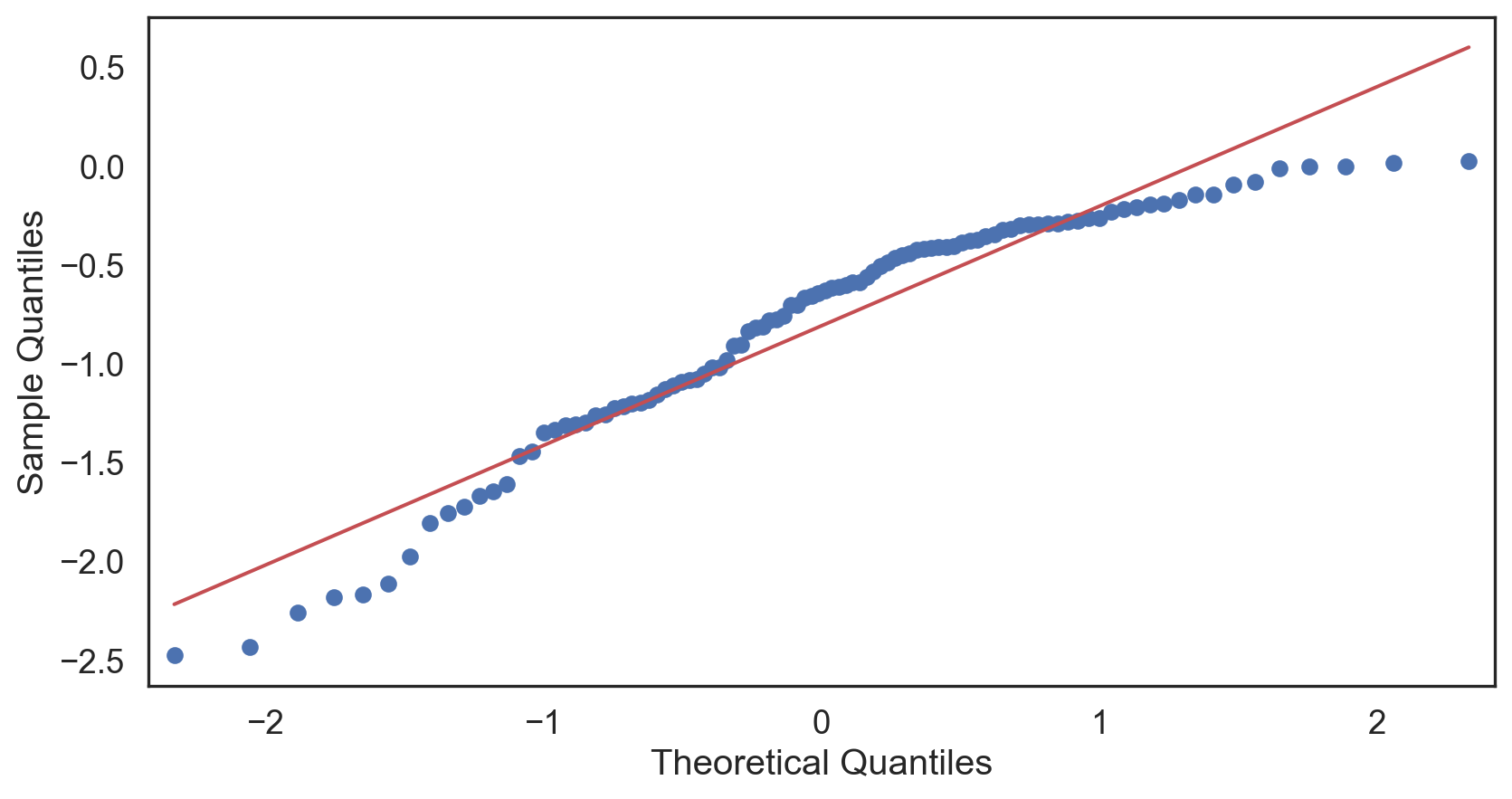
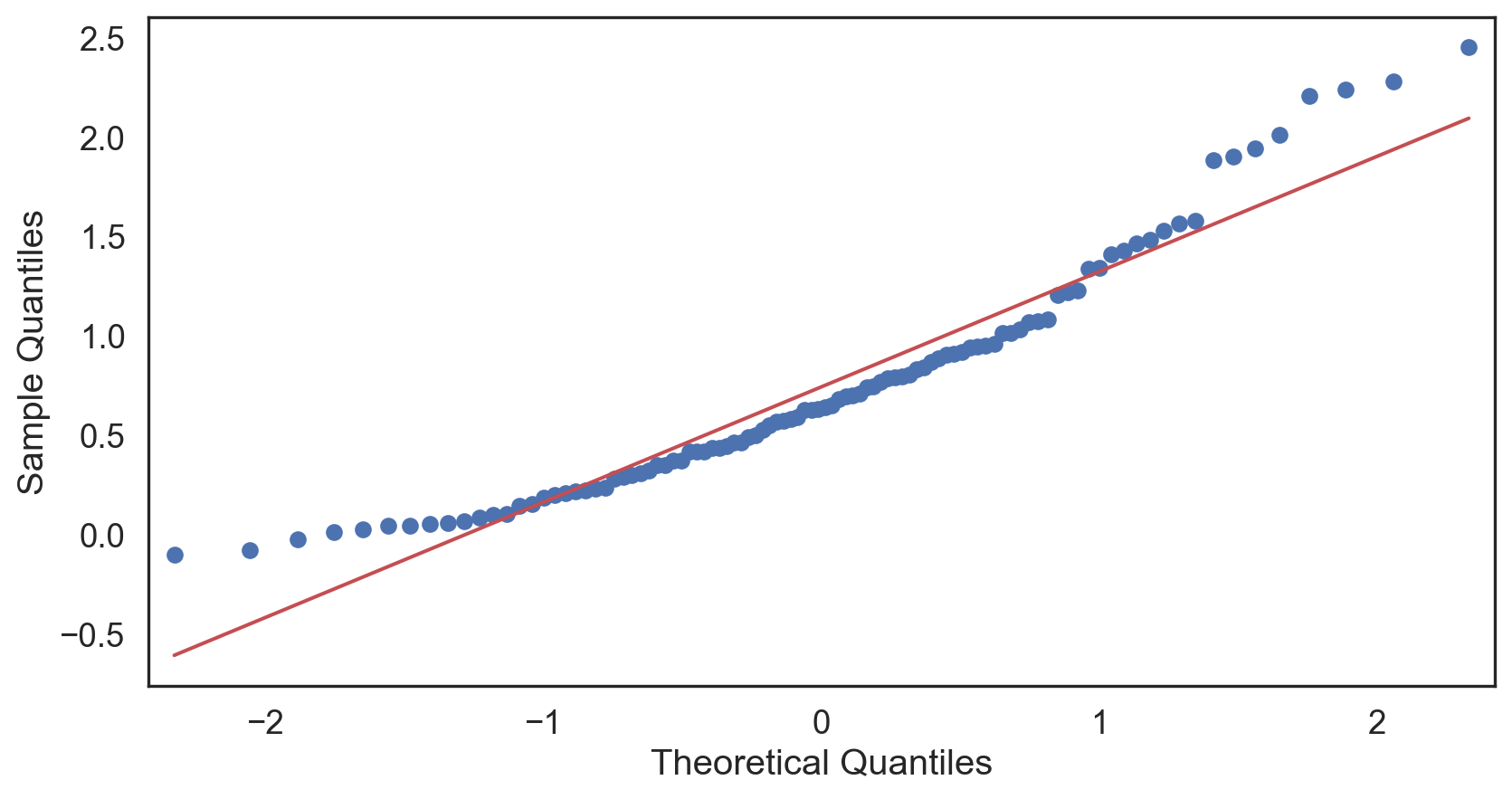
Q-Q plot

Testing normality: data shape

Code 
# Make a copy of the data 
dataCopy = births14.copy()

# Remove NAs
dataCopyFin = dataCopy.dropna()

# Q-Q plot
sm.qqplot(dataCopyFin.weight, line='s')
plt.title('Newborn Weight Q-Q plot')
plt.show()

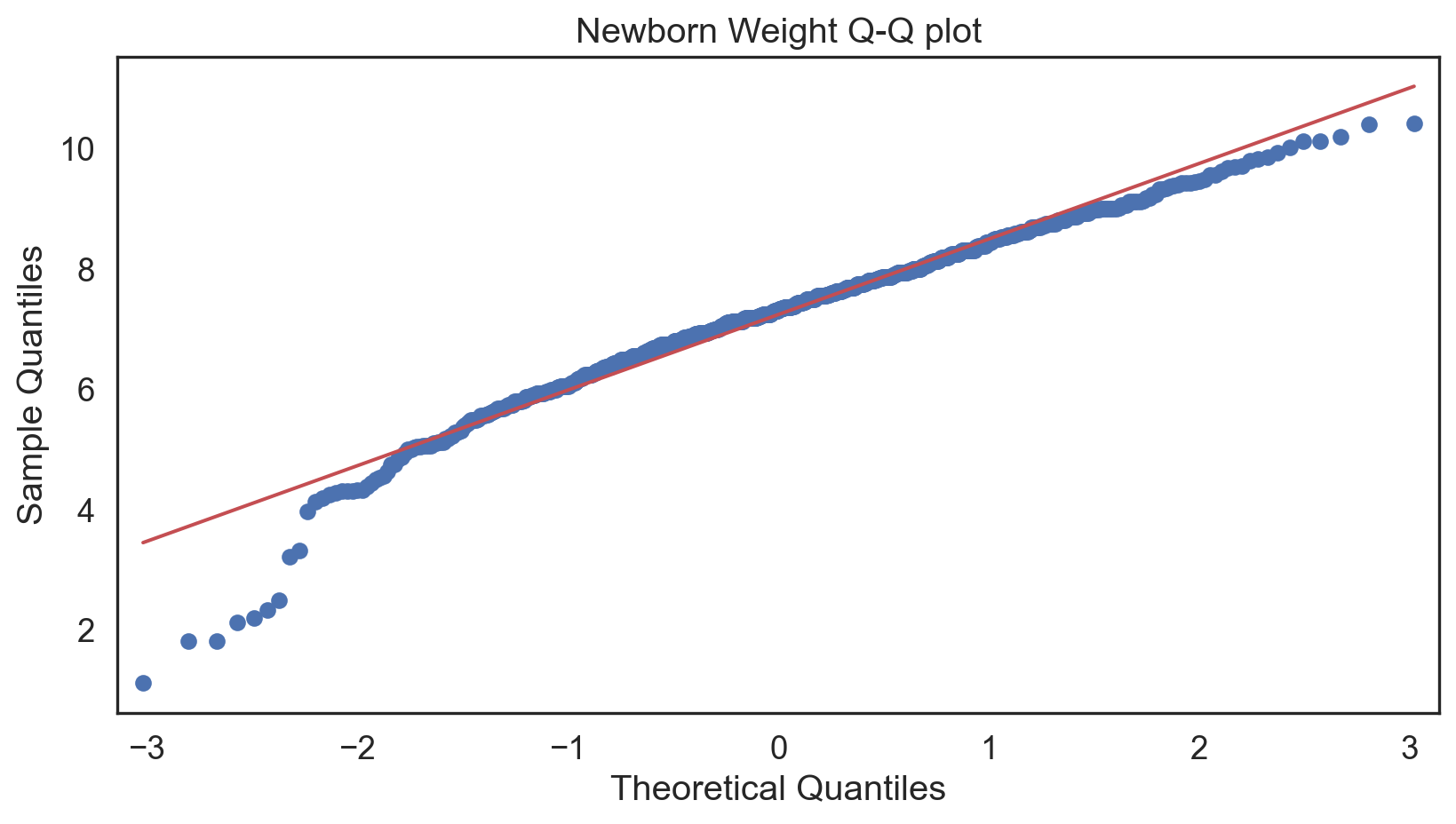
Negative-skew (left-tailed)

Conclusions

  • Always inspect your data first.

  • Visualize relationships and distributions.

  • Identify and handle outliers and missing values.

  • Check for normality and understand the distribution of your data.

We will add to this!

🔗 datasciaz.netlify.app